We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We investigate zero-temperature dynamics for a homogeneous ferromagnetic Ising model on the homogeneous tree of degree three (𝕋) with random (i.i.d. Bernoulli) spin configuration at time 0. Letting θ denote the probability that any particular vertex has a +1 initial spin, for 
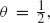infinite spin clusters do not exist at time 0 but we show that infinite ‘spin chains’ (doubly infinite paths of vertices with a common spin) exist in abundance at any time ϵ > 0. We study the structure of the subgraph of 𝕋 generated by the vertices in time-ϵ spin chains. We show the existence of a phase transition in the sense that, for some critical θc with 
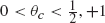spin chains almost surely never form for θ < θc but almost surely do form in finite time for θ > θc. We relate these results to certain quantities of physical interest, such as the t → ∞ asymptotics of the probability 
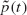that any particular vertex changes spin after time t.
