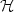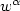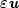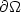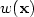A second order Ghost Fluid method is proposed for the treatment of interface problems of elliptic equations with discontinuous coefficients. By appropriate use of auxiliary virtual points, physical jump conditions are enforced at the interface. The signed distance function is used for the implicit description of irregular domain. With the additional unknowns, high order approximation considering the discontinuity can be built. To avoid the ill-conditioned matrix, the interpolation stencils are selected adaptively to balance the accuracy and the numerical stability. Additional equations containing the jump restrictions are assembled with the original discretized algebraic equations to form a new sparse linear system. Several Krylov iterative solvers are tested for the newly derived linear system. The results of a series of 1-D, 2-D tests show that the proposed method possesses second order accuracy in L∞ norm. Besides, the method can be extended to the 3-D problems straightforwardly. Numerical results reveal the present method is highly efficient and robust in dealing with the interface problems of elliptic equations.

Some electromagnetic materials have, in a given frequency range, an effective dielectric permittivity and/or a magnetic permeability which are real-valued negative coefficients when dissipation is neglected. They are usually called metamaterials. We study a scalar transmission problem between a classical dielectric material and a metamaterial, set in an open, bounded subset of Rd, with d = 2,3. Our aim is to characterize occurences where the problem is well-posed within the Fredholm (or coercive + compact) framework. For that, we build some criteria, based on the geometry of the interface between the dielectric and the metamaterial. The proofs combine simple geometrical arguments with the approach of T-coercivity, introduced by the first and third authors and co-worker. Furthermore, the use of localization techniques allows us to derive well-posedness under conditions that involve the knowledge of the coefficients only near the interface. When the coefficients are piecewise constant, we establish the optimality of the criteria.

In studying biomechanical deformation in articular cartilage, the presence of cells (chondrocytes) necessitates the consideration of inhomogeneous elasticity problems in which cells are idealized as soft inclusions within a stiff extracellular matrix. An analytical solution of a soft inclusion problem is derived and used to evaluate iterative numerical solutions of the associated linear algebraic system based on discretization via the finite element method, and use of an iterative conjugate gradient method with algebraic multigrid preconditioning (AMG-PCG). Accuracy and efficiency of the AMG-PCG algorithm is compared to two other conjugate gradient algorithms with diagonal preconditioning (DS-PCG) or a modified incomplete LU decomposition (Euclid-PCG) based on comparison to the analytical solution. While all three algorithms are shown to be accurate, the AMG-PCG algorithm is demonstrated to provide significant savings in CPU time as the number of nodal unknowns is increased. In contrast to the other two algorithms, the AMG-PCG algorithm also exhibits little sensitivity of CPU time and number of iterations to variations in material properties that are known to significantly affect model variables. Results demonstrate the benefits of algebraic multigrid preconditioners for the iterative solution of assembled linear systems based on finite element modeling of soft elastic inclusion problems and may be particularly advantageous for large scale problems with many nodal unknowns.

In this paper, a weighted regularization method for the time-harmonic Maxwell equationswith perfect conducting or impedance boundary condition in composite materials is presented.The computational domain Ω is the unionof polygonal or polyhedral subdomains made of different materials. As a result, the electromagnetic field presents singularitiesnear geometric singularities, which are the interior and exterior edges and corners. The variational formulation of theweighted regularized problem is given on the subspace of ${\cal H}$ ( ${\bf curl}$ ;Ω)whose fields $\textit{\textbf{ u}}$ satisfy $w^\alpha$ div ( $\varepsilon{\textit{\textbf{u}}}$ )∈L2 (Ω) and have vanishing tangential traceor tangential trace in L2 ( $\partial\Omega$ ). The weight function $w(\bf x)$ is equivalentto the distance of $\bf x$ to the geometric singularities and the minimal weight parameter αis given in terms of the singular exponents of a scalar transmission problem.A density result is proven that guarantees the approximability of the solution field by piecewise regular fields.Numerical results for the discretization of the source problemby means of Lagrange Finite Elements of type P 1 and P 2 are given onuniform and appropriately refined two-dimensional meshes.The performance of the method in the case of eigenvalue problems is addressed.