We introduce a stochastic process with discrete time and countable state space that is governed by a sequence of Markov matrices 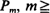 . Each Pm is used for a random number of steps Tm and is then replaced by Pm+1. Tm is a randomized stopping time that may depend on the most recent part of the state history. Thus the global character of the process is non-Markovian.
. Each Pm is used for a random number of steps Tm and is then replaced by Pm+1. Tm is a randomized stopping time that may depend on the most recent part of the state history. Thus the global character of the process is non-Markovian.
This process can be used to model the well-known simulated annealing optimization algorithm with randomized, partly state depending cooling schedules. Generalizing the concept of strong stationary times (Aldous and Diaconis [1]) we are able to show the existence of optimal schedules and to prove some desirable properties. This result is mainly of theoretical interest as the proofs do not yield an explicit algorithm to construct the optimal schedules.

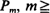 . Each
. Each 