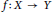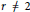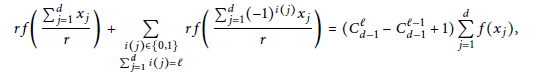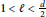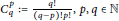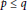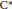1 results
On Ulam Stability of a Functional Equation in Banach Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 173-183
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
-
Let
$X$ and 
$Y$ be Banach spaces and let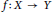 
$f\,:\,X\,\to \,Y$ be an odd mapping. For any rational number 
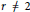$r\,\ne \,2$, C. Baak, D. H. Boo, and Th. M. Rassias proved the Hyers–Ulam stability of the functional equation
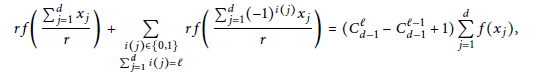$$rf\left( \frac{\sum\nolimits_{j=1}^{d}{{{x}_{j}}}}{r} \right)\,+\,\sum\limits_{\begin{smallmatrix}
i\left( j \right)\,\in \left\{ 0,\,1 \right\} \\
\sum\nolimits_{j=1}^{d}{i\left( j \right)=\ell }
\end{smallmatrix}}{rf\left( \frac{\sum\nolimits_{j=1}^{d}{{{\left( -1 \right)}^{i\left( j \right)}}{{x}_{j}}}}{r} \right)}\,=\,\left( C_{d-1}^{\ell }\,-\,C_{d-1}^{\ell -1}\,+\,1 \right)\,\sum\limits_{j=1}^{d}{f\left( {{x}_{j}} \right),}$$where
$d$ and 
$\ell$ are positive integers so that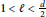 
$1\,<\,\ell \,<\,\frac{d}{2}$, and 
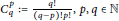$C_{q}^{p}\,:=\frac{q!}{\left( q-p \right)!p!},\,p,\,q\,\in \,\mathbb{N}$ with 
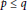$p\,\le \,q$.In this note we solve this equation for arbitrary nonzero scalar
$r$ and show that it is actually
Hyers–Ulam stable. We thus extend and generalize Baak et al.’s result. Other questions concerning
the 
$^{*}$-homomorphisms and the multipliers between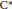 
${{C}^{*}}$-algebras are also considered.
