We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The dimensions of the graded quotients of the cohomology of a plane curve complement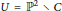 
$U\,=\,{{\mathbb{P}}^{2}}\,\backslash \,C$ with respect to the Hodge filtration are described in terms of simple geometrical invariants. The case of curves with ordinary singularities is discussed in detail. We also give a precise numerical estimate for the difference between the Hodge filtration and the pole order filtration on 
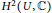${{H}^{2}}\left( U,\,\mathbb{C} \right)$.
