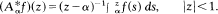2 results
Corrigendum to “Generalized Cesàro Matrices”
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, p. 196
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
Generalized Cesàro Matrices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 4 / 01 December 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 417-422
- Print publication:
- 01 December 1984
-
- Article
-
- You have access
- Export citation

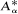 is the operator formally defined on the Hardy space
is the operator formally defined on the Hardy space