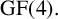1 results
COMPLEX WEIGHING MATRICES AND QUATERNARY CODES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 22 October 2024, pp. 1-9
-
- Article
- Export citation