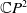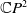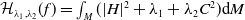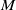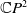2 results
A Helfrich functional for compact surfaces in
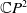 $\mathbb{C}P^{2}$
$\mathbb{C}P^{2}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 04 October 2023, pp. 36-50
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
Global minimizers for axisymmetric multiphasemembranes
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 26 July 2013, pp. 1014-1029
- Print publication:
- October 2013
-
- Article
- Export citation