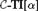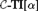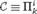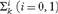2 results
GOODSTEIN SEQUENCES BASED ON A PARAMETRIZED ACKERMANN–PÉTER FUNCTION
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 02 July 2021, pp. 168-186
- Print publication:
- June 2021
-
- Article
- Export citation
A NOTE ON PREDICATIVE ORDINAL ANALYSIS I: ITERATED COMPREHENSION AND TRANSFINITE INDUCTION
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 226-265
- Print publication:
- March 2019
-
- Article
- Export citation