We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let X(t) be a continuous, homogeneous stochastic process with independent increments characterized by a, σ, M, N in the Lévy representation formula. In this note we obtain the Lévy canonical representation of the characteristic function of a stochastic integral (in the sense of convergence in probability) of the form
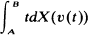(where υ(t) is a non-decreasing, non-negative and left-continuous function) in terms of υ(t), a, σ, M, N.
