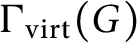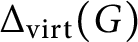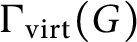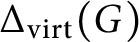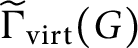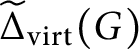2 results
3 - The spread of finite and infinite groups
-
-
- Book:
- Groups St Andrews 2022 in Newcastle
- Published online:
- 21 November 2024
- Print publication:
- 12 December 2024, pp 74-117
-
- Chapter
- Export citation
The virtually generating graph of a profinite group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 15 October 2020, pp. 808-819
- Print publication:
- December 2021
-
- Article
- Export citation