1 results
Resolvent operators of Markov processes and their applications in the control of a finite dam
-
- Journal:
- Journal of Applied Probability / Volume 26 / Issue 2 / June 1989
- Published online by Cambridge University Press:
- 14 July 2016, pp. 314-324
- Print publication:
- June 1989
-
- Article
- Export citation
-
The resolvent operators of the following two processes are obtained: (a) the bivariate Markov process W = (X, Y), where Y(t) is an irreducible Markov chain and X(t) is its integral, and (b) the geometric Wiener process G(t) = exp{B(t} where B(t) is a Wiener process with non-negative drift μ and variance parameter σ2. These results are then used via a limiting procedure to determine the long-run average cost per unit time of operating a finite dam where the input process is either X(t) or G(t). The system is controlled by a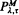
policy (Attia [1], Lam [6]).
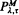policy (Attia [1], Lam [6]).