We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
$\ell _p$ spaces
In this paper, we present a characterization of strong subdifferentiability of the norm of bounded linear operators on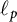 
$\ell _p$ spaces, 
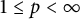$1\leq p<\infty $. Furthermore, we prove that the set of all bounded linear operators in 
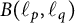${B}(\ell _p, \ell _q)$ for which the norm of 
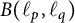${B}(\ell _p, \ell _q)$ is strongly subdifferentiable is dense in 
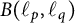${B}(\ell _p, \ell _q)$. Additionally, we present a characterization of Fréchet differentiability of the norm of bounded linear operators from 
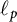$\ell _p$ to 
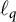$\ell _q$, where 
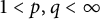$1 < p, q < \infty $. Applying this result, we will show that the Fréchet differentiability and the Gateaux differentiability of the norm of bounded linear operators on 
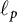$\ell _p$ spaces coincide, extending a known theorem regarding the operator norm on Hilbert 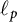spaces.
