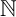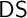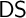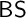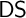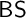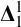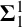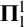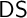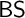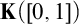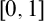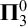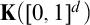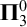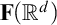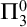This thesis is devoted to the exploration of the complexity of some mathematical problems using the framework of computable analysis and (effective) descriptive set theory. We will especially focus on Weihrauch reducibility as a means to compare the uniform computational strength of problems. After a short introduction of the relevant background notions, we investigate the uniform computational content of problems arising from theorems that lie at the higher levels of the reverse mathematics hierarchy.
We first analyze the strength of the open and clopen Ramsey theorems. Since there is not a canonical way to phrase these theorems as multi-valued functions, we identify eight different multi-valued functions (five corresponding to the open Ramsey theorem and three corresponding to the clopen Ramsey theorem) and study their degree from the point of view of Weihrauch, strong Weihrauch, and arithmetic Weihrauch reducibility.
We then discuss some new operators on multi-valued functions and study their algebraic properties and the relations with other previously studied operators on problems. In particular, we study the first-order part and the deterministic part of a problem f, capturing the Weihrauch degree of the strongest multi-valued problem that is reducible to f and that, respectively, has codomain 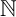 $\mathbb {N}$
or is single-valued.
$\mathbb {N}$
or is single-valued.
These notions proved to be extremely useful when exploring the Weihrauch degree of the problem 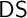 $\mathsf {DS}$
of computing descending sequences in ill-founded linear orders. They allow us to show that
$\mathsf {DS}$
of computing descending sequences in ill-founded linear orders. They allow us to show that 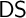 $\mathsf {DS}$
, and the Weihrauch equivalent problem
$\mathsf {DS}$
, and the Weihrauch equivalent problem 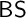 $\mathsf {BS}$
of finding bad sequences through non-well quasi-orders, while being very “hard” to solve, are rather weak in terms of uniform computational strength. We then generalize
$\mathsf {BS}$
of finding bad sequences through non-well quasi-orders, while being very “hard” to solve, are rather weak in terms of uniform computational strength. We then generalize 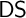 $\mathsf {DS}$
and
$\mathsf {DS}$
and 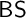 $\mathsf {BS}$
by considering
$\mathsf {BS}$
by considering  $\boldsymbol {\Gamma }$
-presented orders, where
$\boldsymbol {\Gamma }$
-presented orders, where  $\boldsymbol {\Gamma }$
is a Borel pointclass or
$\boldsymbol {\Gamma }$
is a Borel pointclass or 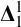 $\boldsymbol {\Delta }^1_1$
,
$\boldsymbol {\Delta }^1_1$
, 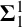 $\boldsymbol {\Sigma }^1_1$
,
$\boldsymbol {\Sigma }^1_1$
, 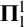 $\boldsymbol {\Pi }^1_1$
. We study the obtained
$\boldsymbol {\Pi }^1_1$
. We study the obtained 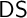 $\mathsf {DS}$
-hierarchy and
$\mathsf {DS}$
-hierarchy and 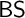 $\mathsf {BS}$
-hierarchy of problems in comparison with the (effective) Baire hierarchy and show that they do not collapse at any finite level.
$\mathsf {BS}$
-hierarchy of problems in comparison with the (effective) Baire hierarchy and show that they do not collapse at any finite level.
Finally, we work in the context of geometric measure theory and we focus on the characterization, from the point of view of descriptive set theory, of some conditions involving the notions of Hausdorff/Fourier dimension and Salem sets. We first work in the hyperspace 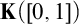 $\mathbf {K}([0,1])$
of compact subsets of
$\mathbf {K}([0,1])$
of compact subsets of 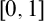 $[0,1]$
and show that the closed Salem sets form a
$[0,1]$
and show that the closed Salem sets form a 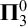 $\boldsymbol {\Pi }^0_3$
-complete family. This is done by characterizing the complexity of the family of sets having sufficiently large Hausdorff or Fourier dimension. We also show that the complexity does not change if we increase the dimension of the ambient space and work in
$\boldsymbol {\Pi }^0_3$
-complete family. This is done by characterizing the complexity of the family of sets having sufficiently large Hausdorff or Fourier dimension. We also show that the complexity does not change if we increase the dimension of the ambient space and work in 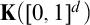 $\mathbf {K}([0,1]^d)$
. We also generalize the results by relaxing the compactness of the ambient space and show that the closed Salem sets are still
$\mathbf {K}([0,1]^d)$
. We also generalize the results by relaxing the compactness of the ambient space and show that the closed Salem sets are still 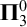 $\boldsymbol {\Pi }^0_3$
-complete when we endow
$\boldsymbol {\Pi }^0_3$
-complete when we endow 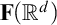 $\mathbf {F}(\mathbb {R}^d)$
with the Fell topology. A similar result holds also for the Vietoris topology.
$\mathbf {F}(\mathbb {R}^d)$
with the Fell topology. A similar result holds also for the Vietoris topology.
We conclude by analyzing the same notions from the point of view of effective descriptive set theory and Type-2 Theory of Effectivity, and show that the complexities remain the same also in the lightface case. In particular, we show that the family of all the closed Salem sets is 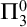 $\Pi ^0_3$
-complete. We furthermore characterize the Weihrauch degree of the functions computing Hausdorff and Fourier dimension of closed sets.
$\Pi ^0_3$
-complete. We furthermore characterize the Weihrauch degree of the functions computing Hausdorff and Fourier dimension of closed sets.
Abstract prepared by Manlio Valenti.
E-mail:[email protected]