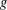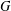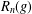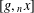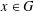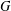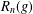Let $g$ be an element of a finite group $G$ and let $R_{n}(g)$ be the subgroup generated by all the right Engel values $[g,_{n}x]$ over $x\in G$. In the case when $G$ is soluble we prove that if, for some $n$, the Fitting height of $R_{n}(g)$ is equal to 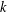$k$, then 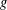$g$ belongs to the 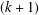$(k+1)$th Fitting subgroup 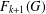$F_{k+1}(G)$. For nonsoluble 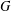$G$, it is proved that if, for some $n$, the generalized Fitting height of 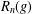$R_{n}(g)$ is equal to 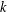$k$, then 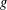$g$ belongs to the generalized Fitting subgroup 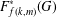$F_{f(k,m)}^{\ast }(G)$ with 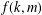$f(k,m)$ depending only on 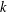$k$ and $m$, where 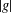$|g|$ is the product of $m$ primes counting multiplicities. It is also proved that if, for some $n$, the nonsoluble length of 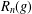$R_{n}(g)$ is equal to 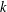$k$, then 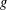$g$ belongs to a normal subgroup whose nonsoluble length is bounded in terms of 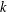$k$ and $m$. Earlier, similar generalizations of Baer’s theorem (which states that an Engel element of a finite group belongs to the Fitting subgroup) were obtained by the first two authors in terms of left Engel-type subgroups.

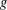
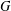
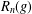
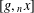
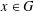
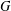
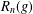
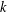
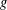
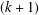
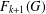
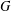
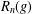
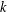
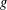
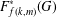
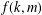
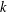
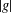
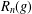
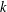
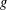
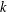
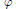Suppose that a finite group G admits an automorphism of order 2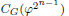n such that the fixed-point subgroup of the involution 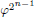is nilpotent of class 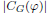c. Let m = ) be the number of fixed points of . It is proved that G has a characteristic soluble subgroup of derived length bounded in terms of n, c whose index is bounded in terms of m, n, c. A similar result is also proved for Lie rings.