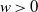We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We analyze the process M(t) representing the maximum of the one-dimensional telegraph process X(t) with exponentially distributed upward random times and generally distributed downward random times. The evolution of M(t) is governed by an alternating renewal of two phases: a rising phase R and a constant phase C. During a rising phase, X(t) moves upward, whereas, during a constant phase, it moves upward and downward, continuing to move until it attains the maximal level previously reached. Under some choices of the distribution of the downward times, we are able to determine the distribution of C, which allows us to obtain some bounds for the survival function of M(t). In the particular case of exponential downward random times, we derive an explicit expression for the survival function of M(t). Finally, the moments of the first passage time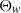 
$\Theta_w$ of the process X(t) through a fixed boundary 
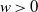$w>0$ are analyzed.
