We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The word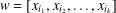 
$w=[x_{i_{1}},x_{i_{2}},\ldots ,x_{i_{k}}]$ is a simple commutator word if 
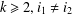$k\geq 2,i_{1}\neq i_{2}$ and 
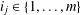$i_{j}\in \{1,\ldots ,m\}$ for some 
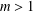$m>1$. For a finite group 
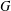$G$, we prove that if 
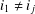$i_{1}\neq i_{j}$ for every 
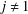$j\neq 1$, then the verbal subgroup corresponding to 
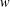$w$ is nilpotent if and only if 
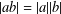$|ab|=|a||b|$ for any 
$w$-values 
$a,b\in G$ of coprime orders. We also extend the result to a residually finite group 
$G$, provided that the set of all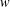 
$w$-values in 
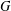$G$ is finite.
