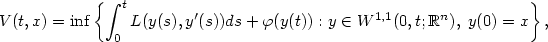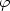We investigate the value function of the Bolza problem of the Calculus of Variations
$$ V (t,x)=\inf \left\{ \int_{0}^{t} L (y (s),y' (s))ds + \varphi (y(t)) : y \in W^{1,1} (0,t;\mathbb{R}^n),\; y(0)=x \right\},$$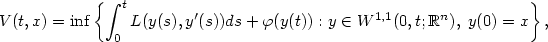 with a lower semicontinuous Lagrangian L and a final cost $ \varphi $, and show that it is locally Lipschitz for t>0 whenever L is locally bounded. It also satisfies Hamilton-Jacobi inequalities in a generalized sense. When the Lagrangian is continuous, then the value function is the unique lower semicontinuous solution to the corresponding Hamilton-Jacobi equation, while for discontinuous Lagrangian we characterize the value function by using the so called contingent inequalities.