A shared ledger is a record of transactions that can be updated by any member of a group of users. The notion of independent and consistent record-keeping in a shared ledger is important for blockchain and more generally for distributed ledger technologies. In this paper we analyze a stochastic model for the shared ledger known as the tangle, which was devised as the basis for the IOTA cryptocurrency. The model is a random directed acyclic graph, and its growth is described by a non-Markovian stochastic process. We first prove ergodicity of the stochastic process, and then derive a delay differential equation for the fluid model which describes the tangle at high arrival rate. We prove convergence in probability of the tangle process to the fluid model, and also prove global stability of the fluid model. The convergence proof relies on martingale techniques.

We prove that for the linear scalar delay differential equation

$$\dot{x}\left( t \right)=-a\left( t \right)x\left( t \right)+b\left( t \right)x\left( t-1 \right)$$

with non-negative periodic coefficients of period $p\,>\,0$, the stability threshold for the trivial solution is $r\,:=\int_{0}^{p}{\left( b\left( t \right)-a\left( t \right) \right)}dt\,=\,0$, assuming that $b\left( t+1 \right)-a\left( t \right)$ does not change its sign. By constructing a class of explicit examples, we show the counter-intuitive result that, in general, $r\,=\,0$ is not a stability threshold.

The aim of this paper is to give a detailed analysis of Hopf bifurcation of a ratio-dependent predator–prey system involving two discrete delays. A delay parameter is chosen as the bifurcation parameter for the analysis. Stability of the bifurcating periodic solutions is determined by using the centre manifold theorem and the normal form theory introduced by Hassard et al. Some of the bifurcation properties including the direction, stability and period are given. Finally, our theoretical results are supported by some numerical simulations.

The stochastic dynamics of chemical reactions can be accurately described by chemicalmaster equations. An approximated time-evolution equation of the Langevin type has beenproposed by Gillespie based on two explicit dynamical conditions. However, whennumerically solve these chemical Langevin equations, we often have a small stopping time–atime point of having an unphysical solution–in the case of low molecular numbers. Thispaper proposes an approach to simulate stochasticities in chemical reactions withdeterministic delay differential equations. We introduce a deterministic Brownian motiondescribed by delay differential equations, and replace the Gaussian noise in the chemicalLangevin equations by the solutions of these deterministic equations. This modificationcan largely increase the stopping time in simulations and regain the accuracy as in thechemical Langevin equations. The novel aspect of the present study is to apply thedeterministic Brownian motion to chemical reactions. It suggests a possible direction ofdeveloping a hybrid method of simulating dynamic behaviours of complex gene regulationnetworks.

Biological rhythms occur at different levels in the organism. In single cells, the celldivision cycle shows rhythmicity in the way its molecular regulators, the cyclin dependantkinases (CDKs), modulate their activity periodically to ensure a healthy progression. Intissues, cell proliferation is driven by the circadian clock, which modulates theprogression through the cell cycle along the day. The circadian clock shows endogenousrhythmicity through a robust network of transcription-translation feedback loops thatcreate sustained oscillations. Rhythmicity is preserved in cell populations by thecoordination of the clocks among cells, through rhythmic synchronization signals. Here wediscuss mechanisms for generating rhythmic activities in cell populations by reviewingsome of the mathematical models that deal with them. We discuss the implication ofbiological rhythms for tissue growth and the possible application to chronomodulatedcancer treatments.

The aim of this paper is to study the steady states of the mathematical models with delaykernels which describe pathogen-immune dynamics of infectious diseases. In the study of mathematicalmodels of infectious diseases it is important to predict whether the infection disappearsor the pathogens persist. The delay kernel is described by the memory function that reflects theinfluence of the past density of pathogen in the blood and it is given by a nonnegative bounded andnormated function k defined on [ 0, ∞ ). By using the coefficient of the kernel k, as a bifurcationparameter, the models are found to undergo a sequence of Hopf bifurcation. The direction and the stability criteria of bifurcation periodic solutions are obtained by applying the normal form theory and the center manifold theorems. Some numerical simulation examples for justifying the theoretical results are also given.

Second-order linear (non-autonomous as well as autonomous) delay differential equations of unstable type are considered. In the non-autonomous case, sufficient conditions are given in order that all oscillatory solutions are bounded or all oscillatory solutions tend to zero at $\infty$. In the case where the equations are autonomous, necessary and sufficient conditions are established for all oscillatory solutions to be bounded or all oscillatory solutions to tend to zero at $\infty$.

We propose a new model for the Stumpy Induction Factor-induced slender to stumpy transformation of Trypanosoma brucei gambiense cells in immunosuppressed mice. The model is a set of delay differential equations that describe the time-course of the infection. We fit the model, using a maximum-likelihood method, to previously published data on parasitaemia in four mice. The model is shown to be a good fit and parameter estimates and confidence intervals are derived. Our estimated parameter values are consistent with estimates from previous experimental studies. The model predicts the following. Slender cells can be classified as uncommitted, committed and dividing, and committed and non-dividing. A committed slender cell undergoes about 5 divisions before exiting the cell-cycle. Committed slender cells must produce SIF, and stumpy cells must not produce SIF. There are two mechanisms for differentiation, a background differentiation rate, and a SIF-concentration-dependent differentiation rate, which is proportional to SIF concentration. SIF has a half-life of about 1·4 h in mice. We also show, with suitable changes in the parameter values, that the model reflects behaviours seen in other host species and trypanosome strains.

A new oscillation criterion is given for the delay differential equation ${x}'\,(t)\,+\,p(t)x\,(t\,-\,\text{ }\!\!\tau\!\!\text{ (t)})\,=\,0$, where 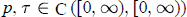$p,\,\text{ }\!\!\tau\!\!\text{ }\,\in \,\text{C}\,\text{( }\!\![\!\!\text{ 0,}\,\infty ),\,\text{ }\!\![\!\!\text{ 0,}\,\infty )\text{)}$ and the function $T$ defined by 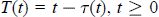$T(t)\,=\,t-\,\text{ }\!\!\tau\!\!\text{ }\,\text{(t),}\,\text{t}\ge \,\text{0}$ is increasing and such that 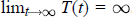${{\lim }_{t\to \infty }}\,T(t)\,=\,\infty $. This criterion concerns the case where 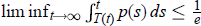$\lim \,{{\inf }_{t\to \infty }}\int _{T(t)}^{t}p(s)ds\le \frac{1}{e}$.

Consider the delay differential equation

where α(t) and β(t) are positive, periodic, and continuous functions with period w > 0, and m is a nonnegative integer. We show that this equation has a positive periodic solution x*(t) with period w. We also establish a necessary and sufficient condition for every solution of the equation to oscillate about x*(t) and a sufficient condition for x*(t) to be a global attractor of all solutions of the equation.