Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T07:04:16.321Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability Threshold for Scalar Linear Periodic Delay Differential Equations

Published online by Cambridge University Press:  20 November 2018

Kyeongah Nah  and
Gergely Röst
Kyeongah Nah
Affiliation:
Bolyai Institute, University of Szeged, Szeged H-6720, Aradi vértanúk tere 1., Hungary e-mail: [email protected] e-mail: [email protected]
Gergely Röst
Affiliation:
Bolyai Institute, University of Szeged, Szeged H-6720, Aradi vértanúk tere 1., Hungary e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that for the linear scalar delay differential equation

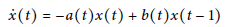$$\dot{x}\left( t \right)=-a\left( t \right)x\left( t \right)+b\left( t \right)x\left( t-1 \right)$$

with non-negative periodic coefficients of period 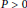$p\,>\,0$, the stability threshold for the trivial solution is 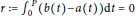$r\,:=\int_{0}^{p}{\left( b\left( t \right)-a\left( t \right) \right)}dt\,=\,0$, assuming that 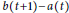$b\left( t+1 \right)-a\left( t \right)$ does not change its sign. By constructing a class of explicit examples, we show the counter-intuitive result that, in general, 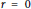$r\,=\,0$ is not a stability threshold.

Keywords

34K2034K06delay differential equationstabilityperiodic system
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 4 , 01 December 2016 , pp. 849 - 857
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Bacaër, N. and Guernaoui, S., The epidemic threshold of vector-borne diseases with seasonality: the case of cutaneous leishmaniasis in Chichaoua, Morocco. J. Math. Biol. 53(2006), 421–436. http://dx.doi.Org/10.1007/s00285-006-0015-0 Google Scholar
[2] Busenberg, S. and Cooke, K. L., Periodic solutions of a periodic nonlinear delay differential equation. SIAM J. Appl. Math. 35(1978), no. 4, 704–721. http://dx.doi.Org/10.1137/0135059 Google Scholar
[3] Chen, Y. and Wu, J., Threshold dynamics of scalar linear periodic delay-differential equations. In: Infinite dimensional dynamical systems. Fields Inst. Commun. 64. Springer, New York, 2013, pp. 269–278.Google Scholar
[4] Hale, J. K. and Verduyn-Lunel, S., Introduction to functional differential equations. Applied Mathematical Sciences 99. Springer-Verlag, New York, 1993.Google Scholar
[5] Hatvani, L. and Krisztin, T., Asymptotic stability for a differential-difference equation containing terms with and without a delay. Acta Sci. Math. (Szeged) 60(2009), 371–384.Google Scholar
[6] Lou, Y. and Zhao, X.-Q., Threshold dynamics in a time-delayed periodic SIS epidemic model. Discrete Contin. Dyn. Syst. Ser. B 12(2009), 169–186. http://dx.doi.Org/10.3934/dcdsb.2009.12.169 Google Scholar
[7] Röst, G., Neimark-Sacker bifurcation for periodic delay differential equations. Nonlinear Anal. 60(2005), no. 6, 1025–1044. http://dx.doi.Org/10.1016/j.na.2004.08.043 Google Scholar
[8] Smith, H. L., An introduction to delay differential equations with applications to the life sciences. Texts in Applied Mathematics 57. Springer, New York, 2011.Google Scholar
[9] Wang, W. and Zhao, X.-Q., Threshold dynamics for compartmental epidemic models in periodic environments. J. Dynam. Differential Equations 20(2008), no. 3, 699–717. http://dx.doi.Org/10.1007/s10884-008-9111-8 Google Scholar
[10] Xu, D. and Zhao, X.-Q., Dynamics in a periodic competitive model with stage structure. J. Math. Anal. Appl. 311(2005), no. 2, 417–438. http://dx.doi.Org/10.1016/j.jmaa.2005.02.062 Google Scholar
[11] Zhao, X.-Q.. Basic reproduction ratios for periodic compartmental models with time delays. J. Dynam. Differential Equations, to appear. doi:10.1007/sl0884-015-9425-2, 2016Google Scholar