Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T04:53:01.556Z Has data issue: false hasContentIssue false
  • English
  • Français

An Oscillation Criterion for First Order Linear Delay Differential Equations

Published online by Cambridge University Press:  20 November 2018

CH. G. Philos  and
Y. G. Sficas
CH. G. Philos
Affiliation:
Department of Mathematics University of Ioannina P.O. Box 1186 451 10 Ioannina Greece
Y. G. Sficas
Affiliation:
Department of Mathematics University of Ioannina P.O. Box 1186 451 10 Ioannina Greece
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A new oscillation criterion is given for the delay differential equation ${x}'\,(t)\,+\,p(t)x\,(t\,-\,\text{ }\!\!\tau\!\!\text{ (t)})\,=\,0$, where 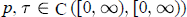$p,\,\text{ }\!\!\tau\!\!\text{ }\,\in \,\text{C}\,\text{( }\!\![\!\!\text{ 0,}\,\infty ),\,\text{ }\!\![\!\!\text{ 0,}\,\infty )\text{)}$ and the function $T$ defined by 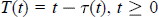$T(t)\,=\,t-\,\text{ }\!\!\tau\!\!\text{ }\,\text{(t),}\,\text{t}\ge \,\text{0}$ is increasing and such that 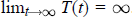${{\lim }_{t\to \infty }}\,T(t)\,=\,\infty $. This criterion concerns the case where 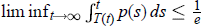$\lim \,{{\inf }_{t\to \infty }}\int _{T(t)}^{t}p(s)ds\le \frac{1}{e}$.

Keywords

34K15Delay differential equationoscillation
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 2 , 01 June 1998 , pp. 207 - 213
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Elbert, Á. and Stavroulakis, I. P., Oscillations of first order differential equations with deviating arguments. World Sci. Ser. Appl. Anal., Vol. 1, 163–178. World Sci. Publishing, Teaneck, NJ, 1992.Google Scholar
2. Elbert, Á., Oscillation and nonoscillation criteria for delay differential equations. Proc. Amer.Math. Soc. 123 (1995), 1503–1510.Google Scholar
3. Erbe, L. H. and Zhang, B. G., Oscillation for first order linear differential equations with deviating arguments. Differential Integral Equations 1 (1988), 305–314.Google Scholar
4. Györi, I. and Ladas, G., Oscillation Theory of Delay Differential Equations With Applications. Clarendon Press, Oxford, 1991.Google Scholar
5. Koplatadze, R. G. and T.A.Chanturija,On the oscillatory and monotone solutions of first order differential equations with deviating arguments. (Russian) Differentsial’nye Uravneniya 18 (1982), 1463–1465.Google Scholar
6. Kwong, M. K., Oscillation of first-order delay equations. J. Math. Anal. Appl. 156 (1991), 274–286.Google Scholar
7. Ladas, G., Sharp conditions for oscillations caused by delays. Appl. Anal. 9 (1979), 93–98.Google Scholar
8. Ladas, G., Lakshmikantham, V. and Papadakis, J. S., Oscillations of higher-order retarded differential equations generated by the retarded argument. In: Delay and Functional Differential Equations and their Applications. Academic Press, New York, 1972, 219–231.Google Scholar
9. Ladde, G. S., Lakshmikantham, V. and Zhang, B. G., Oscillation Theory of Differential Equations with Deviating Arguments. Marcel Dekker, Inc., New York, 1987.Google Scholar