4 results
On Generating Functions of Waiting Times and Numbers of Occurrences of Compound Patterns in a Sequence of Multistate Trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 71-81
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
On ordered series and later waiting time distributions in a sequence of Markov dependent multistate trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 623-642
- Print publication:
- September 2003
-
- Article
- Export citation
On probability generating functions for waiting time distributions of compound patterns in a sequence of multistate trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 70-80
- Print publication:
- March 2002
-
- Article
- Export citation
Distribution of the scan statistic for a sequence of bistate trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 908-916
- Print publication:
- December 2001
-
- Article
- Export citation

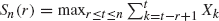 be the scan statistic of window size
be the scan statistic of window size 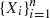 . The scan statistic
. The scan statistic 