1 results
A note on the column–row property
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1244-1254
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
In this article, we study the following question asked by Michael Hartz in a recent paper (Every complete Pick space satisfies the column-row property, to appear in Acta Mathematica): which operator spaces satisfy the column–row property? We provide a complete classification of the column–row property (CRP) for noncommutative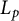
$L_{p}$-spaces over semifinite von Neumann algebras. We study other relevant properties of operator spaces that are related to the CRP and discuss their existence and nonexistence for various natural examples of operator spaces.
