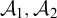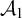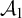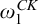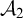We ask when, for a pair of structures 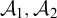 $\mathcal {A}_1,\mathcal {A}_2$
, there is a uniform effective procedure that, given copies of the two structures, unlabeled, always produces a copy of
$\mathcal {A}_1,\mathcal {A}_2$
, there is a uniform effective procedure that, given copies of the two structures, unlabeled, always produces a copy of 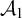 $\mathcal {A}_1$
. We give some conditions guaranteeing that there is such a procedure. The conditions might suggest that for the pair of orderings
$\mathcal {A}_1$
. We give some conditions guaranteeing that there is such a procedure. The conditions might suggest that for the pair of orderings 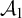 $\mathcal {A}_1$
of type
$\mathcal {A}_1$
of type 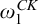 $\omega _1^{CK}$
and
$\omega _1^{CK}$
and 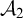 $\mathcal {A}_2$
of Harrison type, there should not be any such procedure, but, in fact, there is one. We construct an example for which there is no such procedure. The construction involves forcing. On the way to constructing our example, we prove a general result on modifying Cohen generics.
$\mathcal {A}_2$
of Harrison type, there should not be any such procedure, but, in fact, there is one. We construct an example for which there is no such procedure. The construction involves forcing. On the way to constructing our example, we prove a general result on modifying Cohen generics.