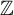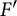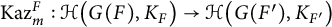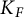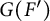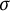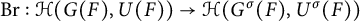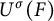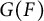Let G be a split connected reductive group defined over 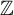 $\mathbb {Z}$. Let F and
$\mathbb {Z}$. Let F and 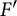 $F'$ be two non-Archimedean m-close local fields, where m is a positive integer. D. Kazhdan gave an isomorphism between the Hecke algebras
$F'$ be two non-Archimedean m-close local fields, where m is a positive integer. D. Kazhdan gave an isomorphism between the Hecke algebras 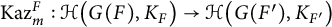 $\mathrm {Kaz}_m^F :\mathcal {H}\big (G(F),K_F\big ) \rightarrow \mathcal {H}\big (G(F'),K_{F'}\big )$, where
$\mathrm {Kaz}_m^F :\mathcal {H}\big (G(F),K_F\big ) \rightarrow \mathcal {H}\big (G(F'),K_{F'}\big )$, where 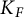 $K_F$ and
$K_F$ and  $K_{F'}$ are the mth usual congruence subgroups of
$K_{F'}$ are the mth usual congruence subgroups of  $G(F)$ and
$G(F)$ and 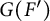 $G(F')$, respectively. On the other hand, if
$G(F')$, respectively. On the other hand, if 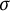 $\sigma $ is an automorphism of G of prime order l, then we have Brauer homomorphism
$\sigma $ is an automorphism of G of prime order l, then we have Brauer homomorphism 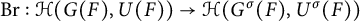 $\mathrm {Br}:\mathcal {H}(G(F),U(F))\rightarrow \mathcal {H}(G^\sigma (F),U^\sigma (F))$, where
$\mathrm {Br}:\mathcal {H}(G(F),U(F))\rightarrow \mathcal {H}(G^\sigma (F),U^\sigma (F))$, where  $U(F)$ and
$U(F)$ and 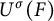 $U^\sigma (F)$ are compact open subgroups of
$U^\sigma (F)$ are compact open subgroups of 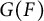 $G(F)$ and
$G(F)$ and  $G^\sigma (F),$ respectively. In this article, we study the compatibility between these two maps in the local base change setting. Further, an application of this compatibility is given in the context of linkage – which is the representation theoretic version of Brauer homomorphism.
$G^\sigma (F),$ respectively. In this article, we study the compatibility between these two maps in the local base change setting. Further, an application of this compatibility is given in the context of linkage – which is the representation theoretic version of Brauer homomorphism.