Stark conjectured that for any $h\in \Bbb {N}$ , there are only finitely many CM-fields with class number h. Let $\mathcal {C}$ be the class of number fields L for which L has an almost normal subfield K such that $L/K$ has solvable Galois closure. We prove Stark’s conjecture for $L\in \mathcal {C}$ of degree greater than or equal to 6. Moreover, we show that the generalised Brauer–Siegel conjecture is true for asymptotically good towers of number fields $L\in \mathcal {C}$ and asymptotically bad families of $L\in \mathcal {C}$ .

For any odd prime $\ell$, let $h_{\ell }(-d)$ denote the $\ell$-part of the class number of the imaginary quadratic field $\mathbb{Q}(\sqrt{-d})$. Nontrivial pointwise upper bounds are known only for $\ell =3$; nontrivial upper bounds for averages of $h_{\ell }(-d)$ have previously been known only for $\ell =3,5$. In this paper we prove nontrivial upper bounds for the average of $h_{\ell }(-d)$ for all primes $\ell \geqslant 7$, as well as nontrivial upper bounds for certain higher moments for all primes $\ell \geqslant 3$.

We prove the finiteness of class numbers and Tate–Shafarevich sets for all affine group schemes of finite type over global function fields, as well as the finiteness of Tamagawa numbers and Godement’s compactness criterion (and a local analogue) for all such groups that are smooth and connected. This builds on the known cases of solvable and semi-simple groups via systematic use of the recently developed structure theory and classification of pseudo-reductive groups.

We study the Stickelberger element of a cyclic extension of global fields of prime power degree. Assuming that S contains an almost splitting place, we show that the Stickelberger element is contained in a power of the relative augmentation ideal whose exponent is at least as large as Gross's prediction. This generalizes the work of Tate (see Section 4) on a refinement of Gross's conjecture in the cyclic case. We also present an example for which Tate's prediction does not hold.

Let D>0 be the fundamental discriminant of a real quadratic field, and h(D) its class number. In this paper, by refining Ono's idea, we show that for any prime p>3, [sharp ]{0<D<X|h(D)[nequiv]0(mod p)}>>p√(X)/logX.

As it had been recognized by Liouville, Hermite, Mordell and others, the number of non-negative integer solutions of the equation in the title is strongly related to the class number of quadratic forms with discriminant —n. The purpose of this note is to point out a deeper relation which makes it possible to derive a reasonable upper bound for the number of solutions.

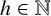
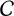
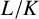
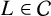
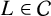
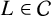
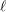
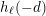
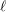
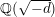
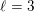
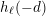
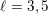
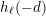
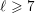
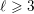
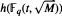Let q be a positive power of an odd prime p, and let Fq(t) be the function field with coefficients in the finite field of q elements. Let denote the ideal class number of the real quadratic function field obtained by adjoining the square root of an even-degree monic 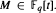. The following theorem is proved: Let n ≧ 1 be an integer not divisible by 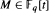p. Then there exist infinitely many monic, squarefree polynomials, such that 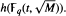n divides the class number, . The proof constructs an element of order n in the ideal class group.