We prove some results concerning convolutions, additive energies, and sumsets of convex sets and their generalizations. In particular, we show that if a set $A\,=\,{{\{{{a}_{1}},\,.\,.\,.\,,\,{{a}_{n}}\}}_{<}}\,\subseteq \,\mathbb{R}$ has the property that for every fixed $1\,\le \,d\,<\,n$, all differences ${{a}_{i}}\,-\,{{a}_{i-d}},\,d\,<\,i\,<n$, are distinct, then $\left| A\,+\,A \right|\,\gg \,{{\left| A \right|}^{3/2+c}}$ for a constant $c\,>\,0$.

A Chebyshev set is a subset of a normed linear space that admits unique best approximations. In the first part of this paper we present some basic results concerning Chebyshev sets. In particular, we investigate properties of the metric projection map, sufficient conditions for a subset of a normed linear space to be a Chebyshev set, and sufficient conditions for a Chebyshev set to be convex. In the second half of the paper we present a construction of a nonconvex Chebyshev subset of an inner product space.

This paper establishes a duality between the category of polytopes (finitely generated real convex sets considered as barycentric algebras) and a certain category of intersections of hypercubes, considered as barycentric algebras with additional constant operations.

We present below a new series of conjectures and openproblems in the fields of (global) Optimization and Matrix analysis, in thesame spirit as our recently published paper [J.-B. Hiriart-Urruty, Potpourri of conjectures and open questions in Nonlinear analysis and Optimization. SIAMReview49 (2007) 255–273]. With each problem come a succinct presentation, a list of specificreferences, and a view on the state of the art of the subject.

The problem of finding geodesics that avoid certain obstacles in negatively curved manifolds has been studied in different situations. In this note we give a generalization of the unclouding theorem of J. Parkkonen and F. Paulin: there is a constant s0=1.534 such that for any Hadamard manifold M with curvature ≤−1 and for any family of disjoint balls or horoballs {Ca}a∈A and for any point p∈M−⋃ a∈ACa if we shrink these balls uniformly by s0 one can always find a geodesic ray emanating from p that avoids the shrunk balls. It will be shown that in the theorem above one can replace the balls by arbitrary convex sets.

Two subsets of the Euclidean plane touch each other if they have a point in common and there is a straight line separating one from the other.

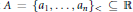
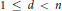
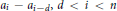
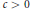
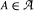It is shown that there exists a positive constant c such that if are families of plane convex sets with for some k ≥ 1 and if every touches every 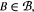then either 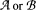contains k members having nonempty intersection.

Linear combinations of exponential distribution functions are considered, and the class of distribution functions so obtainable is investigated. Convex combinations correspond to hyperexponential distributions, while non-convex combinations yield, among other, generalized Erlang distributions obtainable as sums of independent exponential random variables with different parameters.

For a given number n of different exponential distributions, the class investigated is an (n – 1)-dimensional convex subset of the n-dimensional real vector space generated by the n distribution functions. The geometric aspect of this subset is revealed, together with the location of hyperexponential and generalized Erlang distributions.

Kakutani's Theorem states that every point convex and use multifunction ϕ defined on a compact and convex set in a Euclidean space has at least one fixed point. Some necessary conditions are given here which ϕ must satisfy if c is the unique fixed point of ϕ. It is e.g. shown that if the width of ϕ(c) is greater than zero, then ϕ cannot be lsc at c, and if in addition c lies on the boundary of ϕ(c), then there exists a sequence {xk} which converges to c and for which the width of the sets ϕ(xk) converges to zero. If the width of ϕ(c) is zero, then the width of ϕ(xk) converges to zero whenever the sequence {xk} converges to c, but in this case ϕ can be lsc at c.