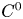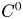We show that the image of a properly embedded Legendrian submanifold under a homeomorphism that is the 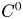 $C^0$-limit of a sequence of contactomorphisms supported in some fixed compact subset is again Legendrian, if the image of the submanifold is smooth. In proving this, we show that any closed non-Legendrian submanifold of a contact manifold admits a positive loop and we provide a parametric refinement of the Rosen–Zhang result on the degeneracy of the Chekanov–Hofer–Shelukhin pseudo-norm for properly embedded non-Legendrians.
$C^0$-limit of a sequence of contactomorphisms supported in some fixed compact subset is again Legendrian, if the image of the submanifold is smooth. In proving this, we show that any closed non-Legendrian submanifold of a contact manifold admits a positive loop and we provide a parametric refinement of the Rosen–Zhang result on the degeneracy of the Chekanov–Hofer–Shelukhin pseudo-norm for properly embedded non-Legendrians.
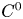 $C^0$-limits of Legendrians and positive loops
$C^0$-limits of Legendrians and positive loops