3 results
A refinement of multivariate Bonferroni-type inequalities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 276-282
- Print publication:
- March 2000
-
- Article
- Export citation
Bonferroni inequalities and deviations of discrete distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 115-121
- Print publication:
- March 1996
-
- Article
- Export citation
On the classical Bonferroni inequalities and the corresponding Galambos inequalities
-
- Journal:
- Journal of Applied Probability / Volume 18 / Issue 3 / September 1981
- Published online by Cambridge University Press:
- 14 July 2016, pp. 757-763
- Print publication:
- September 1981
-
- Article
- Export citation

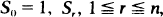 be the sum of the probabilities of all
be the sum of the probabilities of all 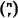 intersections of r events, and
intersections of r events, and 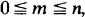 and
and 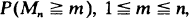 equal to partial sums of series of the form
equal to partial sums of series of the form 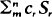 which give the exact probabilities. These inequalities have recently been extended by J. Galambos to give sharper bounds.
which give the exact probabilities. These inequalities have recently been extended by J. Galambos to give sharper bounds.