The Lorenz curve of the distribution of ‘wealth’ is a graph of cumulative proportion of total ‘wealth’ owned, against cumulative proportion of the population owning it. This paper uses Gastwirth's definition of the Lorenz curve which applies to a general probability distribution on (0, ∞) having finite mean; thus it applies both to a ‘population’ distribution 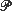 and to empirical distributions obtained on sampling. The Lorenz curves of the latter are proved to converge, with probability 1, uniformly to the former, and similarly for their inverses. Modified Lorenz curves are also defined, which treat atoms of
and to empirical distributions obtained on sampling. The Lorenz curves of the latter are proved to converge, with probability 1, uniformly to the former, and similarly for their inverses. Modified Lorenz curves are also defined, which treat atoms of 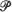 differently, and these and their inverses are proved strongly consistent. Functional central limit theorems are then proved for empirical Lorenz curves and their inverses, under condition that
differently, and these and their inverses are proved strongly consistent. Functional central limit theorems are then proved for empirical Lorenz curves and their inverses, under condition that 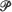 be continuous and have finite variance. A mild variation condition is also needed in some circumstances. If the support of
be continuous and have finite variance. A mild variation condition is also needed in some circumstances. If the support of 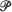 is connected, the weak convergence is relative to C[0, 1] with uniform topology, otherwise to D[0, 1] with M1 topology. Selected applications are discussed, one being to the Gini coefficient.
is connected, the weak convergence is relative to C[0, 1] with uniform topology, otherwise to D[0, 1] with M1 topology. Selected applications are discussed, one being to the Gini coefficient.

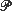 and to empirical distributions obtained on sampling. The Lorenz curves of the latter are proved to converge, with probability 1, uniformly to the former, and similarly for their inverses. Modified Lorenz curves are also defined, which treat atoms of
and to empirical distributions obtained on sampling. The Lorenz curves of the latter are proved to converge, with probability 1, uniformly to the former, and similarly for their inverses. Modified Lorenz curves are also defined, which treat atoms of 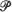 differently, and these and their inverses are proved strongly consistent. Functional central limit theorems are then proved for empirical Lorenz curves and their inverses, under condition that
differently, and these and their inverses are proved strongly consistent. Functional central limit theorems are then proved for empirical Lorenz curves and their inverses, under condition that 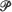 be continuous and have finite variance. A mild variation condition is also needed in some circumstances. If the support of
be continuous and have finite variance. A mild variation condition is also needed in some circumstances. If the support of 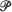 is connected, the weak convergence is relative to
is connected, the weak convergence is relative to 