We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Extending our previous work on eigenvalues of closed surfaces and work of Otal and Rosas, we show that a complete Riemannian surface 
$S$ of finite type and Euler characteristic 
$\unicode[STIX]{x1D712}(S)<0$ has at most 
$-\unicode[STIX]{x1D712}(S)$ small eigenvalues.
Greene and Wu have shown that any continuous strongly convex function on a Riemannian manifold can be uniformly approximated by infinitely differentiable strongly convex functions. This result is not true if the word “strongly” is omitted; in this paper, we give examples of manifolds on which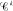 
convex functions cannot be approximated by 
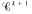convex functions (k = 0, 1,2,...).
