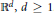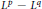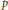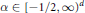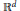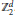We prove qualitatively sharp estimates of the potential kernel for the harmonic oscillator. These bounds are then used to show that the Lp–Lq estimates of the associated potential operator obtained recently by Bongioanni and Torrea are in fact sharp.

We study negative powers of Laguerre differential operators in 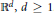${{\mathbb{R}}^{d}},\,d\,\ge \,1$. For these operators we prove two-weight 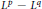$[{{L}^{p}}\,-\,{{L}^{q}}$ estimates with ranges of $q$ depending on 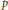$p$. The case of the harmonic oscillator (Hermite operator) has recently been treated by Bongioanni and Torrea by using a straightforward approach of kernel estimates. Here these results are applied in certain Laguerre settings. The procedure is fairly direct for Laguerre function expansions of Hermite type, due to some monotonicity properties of the kernels involved. The case of Laguerre function expansions of convolution type is less straightforward. For half-integer type indices. we transfer the desired results from the Hermite setting and then apply an interpolation argument based on a device we call the convexity principle to cover the continuous range of 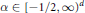$\alpha \,\in \,\,{{[-1/2,\infty )}^{d}}$. Finally, we investigate negative powers of the Dunkl harmonic oscillator in the context of a finite reflection group acting on 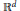${{\mathbb{R}}^{d}}$ and isomorphic to 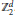$\mathbb{Z}_{2}^{d}$. The two weight 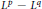${{L}^{p}}\,-\,{{L}^{q}}$ estimates we obtain in this setting are essentially consequences of those for Laguerre function expansions of convolution type.