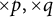 $\times p,\times q$ conjecture
$\times p,\times q$ conjecture
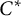 $C^*$-algebras associated with minimal shift spaces
$C^*$-algebras associated with minimal shift spaces
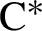 $\mathrm {C}^{\ast }$
-algebras associated with self-similar sets
$\mathrm {C}^{\ast }$
-algebras associated with self-similar sets
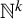 $\mathbb {N}^k$
-actions
$\mathbb {N}^k$
-actions
 $C^*$
-algebra of a homeomorphism
$C^*$
-algebra of a homeomorphism
 $\boldsymbol{C}^*$
-ALGEBRAS ASSOCIATED WITH TWO-SIDED SUBSHIFTS
$\boldsymbol{C}^*$
-ALGEBRAS ASSOCIATED WITH TWO-SIDED SUBSHIFTS
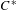 $C^{\ast }$-algebras
$C^{\ast }$-algebras
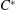 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^*$-ALGEBRAS ARISING FROM
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^*$-ALGEBRAS ARISING FROM 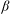 $\beta $-EXPANSIONS
$\beta $-EXPANSIONS