No CrossRef data available.
Article contents
 $\boldsymbol{C}^*$-ALGEBRAS ASSOCIATED WITH TWO-SIDED SUBSHIFTS
$\boldsymbol{C}^*$-ALGEBRAS ASSOCIATED WITH TWO-SIDED SUBSHIFTS
Published online by Cambridge University Press: 18 January 2021
Abstract
This paper is a continuation of the paper, Matsumoto [‘Subshifts,
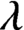 $\lambda $
-graph bisystems and
$\lambda $
-graph bisystems and
 $C^*$
-algebras’, J. Math. Anal. Appl. 485 (2020), 123843]. A
$C^*$
-algebras’, J. Math. Anal. Appl. 485 (2020), 123843]. A
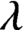 $\lambda $
-graph bisystem consists of a pair of two labeled Bratteli diagrams satisfying a certain compatibility condition on their edge labeling. For any two-sided subshift
$\lambda $
-graph bisystem consists of a pair of two labeled Bratteli diagrams satisfying a certain compatibility condition on their edge labeling. For any two-sided subshift
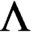 $\Lambda $
, there exists a
$\Lambda $
, there exists a
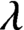 $\lambda $
-graph bisystem satisfying a special property called the follower–predecessor compatibility condition. We construct an AF-algebra
$\lambda $
-graph bisystem satisfying a special property called the follower–predecessor compatibility condition. We construct an AF-algebra
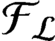 ${\mathcal {F}}_{\mathcal {L}}$
with shift automorphism
${\mathcal {F}}_{\mathcal {L}}$
with shift automorphism
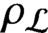 $\rho _{\mathcal {L}}$
from a
$\rho _{\mathcal {L}}$
from a
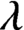 $\lambda $
-graph bisystem
$\lambda $
-graph bisystem
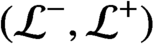 $({\mathcal {L}}^-,{\mathcal {L}}^+)$
, and define a
$({\mathcal {L}}^-,{\mathcal {L}}^+)$
, and define a
 $C^*$
-algebra
$C^*$
-algebra
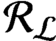 ${\mathcal R}_{\mathcal {L}}$
by the crossed product
${\mathcal R}_{\mathcal {L}}$
by the crossed product
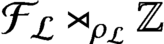 . It is a two-sided subshift analogue of asymptotic Ruelle algebras constructed from Smale spaces. If
. It is a two-sided subshift analogue of asymptotic Ruelle algebras constructed from Smale spaces. If
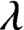 $\lambda $
-graph bisystems come from two-sided subshifts, these
$\lambda $
-graph bisystems come from two-sided subshifts, these
 $C^*$
-algebras are proved to be invariant under topological conjugacy of the underlying subshifts. We present a simplicity condition of the
$C^*$
-algebras are proved to be invariant under topological conjugacy of the underlying subshifts. We present a simplicity condition of the
 $C^*$
-algebra
$C^*$
-algebra
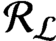 ${\mathcal R}_{\mathcal {L}}$
and the K-theory formulas of the
${\mathcal R}_{\mathcal {L}}$
and the K-theory formulas of the
 $C^*$
-algebras
$C^*$
-algebras
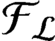 ${\mathcal {F}}_{\mathcal {L}}$
and
${\mathcal {F}}_{\mathcal {L}}$
and
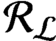 ${\mathcal R}_{\mathcal {L}}$
. The K-group for the AF-algebra
${\mathcal R}_{\mathcal {L}}$
. The K-group for the AF-algebra
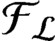 ${\mathcal {F}}_{\mathcal {L}}$
is regarded as a two-sided extension of the dimension group of subshifts.
${\mathcal {F}}_{\mathcal {L}}$
is regarded as a two-sided extension of the dimension group of subshifts.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by Lisa Orloff Clark
The author was supported by JSPS KAKENHI Grant Nos. 15K04896 and 19K03537.



