No CrossRef data available.
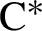 $\mathrm {C}^{\ast }$-algebras associated with self-similar sets
$\mathrm {C}^{\ast }$-algebras associated with self-similar setsPublished online by Cambridge University Press: 01 March 2022
Given a self-similar set K defined from an iterated function system
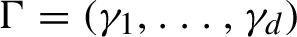 $\Gamma =(\gamma _{1},\ldots ,\gamma _{d})$
and a set of functions
$\Gamma =(\gamma _{1},\ldots ,\gamma _{d})$
and a set of functions
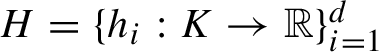 $H=\{h_{i}:K\to \mathbb {R}\}_{i=1}^{d}$
satisfying suitable conditions, we define a generalized gauge action on Kajiwara–Watatani algebras
$H=\{h_{i}:K\to \mathbb {R}\}_{i=1}^{d}$
satisfying suitable conditions, we define a generalized gauge action on Kajiwara–Watatani algebras
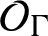 $\mathcal {O}_{\Gamma }$
and their Toeplitz extensions
$\mathcal {O}_{\Gamma }$
and their Toeplitz extensions
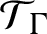 $\mathcal {T}_{\Gamma }$
. We then characterize the KMS states for this action. For each
$\mathcal {T}_{\Gamma }$
. We then characterize the KMS states for this action. For each
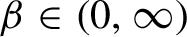 $\beta \in (0,\infty )$
, there is a Ruelle operator
$\beta \in (0,\infty )$
, there is a Ruelle operator
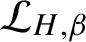 $\mathcal {L}_{H,\beta }$
, and the existence of KMS states at inverse temperature
$\mathcal {L}_{H,\beta }$
, and the existence of KMS states at inverse temperature
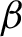 $\beta $
is related to this operator. The critical inverse temperature
$\beta $
is related to this operator. The critical inverse temperature
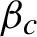 $\beta _{c}$
is such that
$\beta _{c}$
is such that
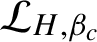 $\mathcal {L}_{H,\beta _{c}}$
has spectral radius 1. If
$\mathcal {L}_{H,\beta _{c}}$
has spectral radius 1. If
 $\beta <\beta _{c}$
, there are no KMS states on
$\beta <\beta _{c}$
, there are no KMS states on
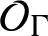 $\mathcal {O}_{\Gamma }$
and
$\mathcal {O}_{\Gamma }$
and
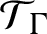 $\mathcal {T}_{\Gamma }$
; if
$\mathcal {T}_{\Gamma }$
; if
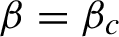 $\beta =\beta _{c}$
, there is a unique KMS state on
$\beta =\beta _{c}$
, there is a unique KMS state on
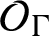 $\mathcal {O}_{\Gamma }$
and
$\mathcal {O}_{\Gamma }$
and
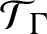 $\mathcal {T}_{\Gamma }$
which is given by the eigenmeasure of
$\mathcal {T}_{\Gamma }$
which is given by the eigenmeasure of
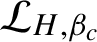 $\mathcal {L}_{H,\beta _{c}}$
; and if
$\mathcal {L}_{H,\beta _{c}}$
; and if
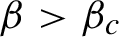 $\beta>\beta _{c}$
, including
$\beta>\beta _{c}$
, including
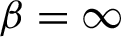 $\beta =\infty $
, the extreme points of the set of KMS states on
$\beta =\infty $
, the extreme points of the set of KMS states on
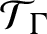 $\mathcal {T}_{\Gamma }$
are parametrized by the elements of K and on
$\mathcal {T}_{\Gamma }$
are parametrized by the elements of K and on
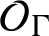 $\mathcal {O}_{\Gamma }$
by the set of branched points.
$\mathcal {O}_{\Gamma }$
by the set of branched points.