Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-25T13:19:37.814Z Has data issue: false hasContentIssue false
  • English
  • Français

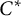A note on the nuclear dimension of Cuntz–Pimsner $C^*$-algebras associated with minimal shift spaces

Part of: Selfadjoint operator algebras Ergodic theory

Published online by Cambridge University Press:  12 December 2022

Zhuofeng He  and
Sihan Wei Open the ORCID record for Sihan Wei [Opens in a new window]
Zhuofeng He
Affiliation:
Research Center for Operator Algebras, East China Normal University, Shanghai, China e-mail: [email protected]
Sihan Wei*
Affiliation:
School of Mathematics and Science, East China Normal University, Shanghai, China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For every minimal one-sided shift space X over a finite alphabet, left special elements are those points in X having at least two preimages under the shift operation. In this paper, we show that the Cuntz–Pimsner 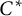$C^*$-algebra 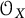$\mathcal {O}_X$ has nuclear dimension 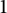$1$ when X is minimal and the number of left special elements in X is finite. This is done by describing concretely the cover of X, which also recovers an exact sequence, discovered before by Carlsen and Eilers.

Keywords

Cuntz–Pimsner algebrasnuclear dimensionminimal shift spaces

MSC classification

Primary: 46L05: General theory of $C^*$-algebras 37A55: Relations with the theory of $C^*$-algebras
Type
Article
Information
Canadian Journal of Mathematics , Volume 76 , Issue 1 , February 2024 , pp. 104 - 125
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The authors were partially supported by a grant from the Shanghai Key Laboratory of PMMP, Science and Technology Commission of Shanghai Municipality (STCSM) (13dz2260400) and by a grant from the NNSF (11531003). The first named author was also supported by Project funded by China Postdoctoral Science Foundation under Grant2020M681221.

References

Bates, T., Carlsen, T., and Eilers, S., Dimension groups associated to  $\beta$ -expansions . Math. Scand. 100(2007), no. 2, 198–208.CrossRefGoogle Scholar
Berthé, V., Steiner, W., and Thuswaldner, J., Multidimensional continued fractions and symbolic codings of toral translations. Preprint, 2021. arXiv:2005.13038v3 Google Scholar
Brix, K., Sturmian subshifts and their ${C}^{\ast }$ -algebras. Preprint, 2021. arXiv:2107.10613v1 Google Scholar
Brix, K. and Carlsen, T., ${C}^{\ast }$ -algebras, groupoids and covers of shift spaces . Trans. Amer. Math. Soc. Ser. B 7(2020), 134–185.CrossRefGoogle Scholar
Carlsen, T., On  ${C}^{\ast }$ -algebras associated with sofic shifts . J. Operator Theory 49(2003), no. 1, 203–212.Google Scholar
Carlsen, T., Symbolic dynamics, partial dynamical systems, Boolean algebras and ${C}^{\ast }$ -algebras generated by partial isometries. Preprint, 2006. arXiv:math/0604165v2 Google Scholar
Carlsen, T., Cuntz–Pimsner  ${C}^{\ast }$ -algebras associated with subshifts . Internat. J. Math. 19(2008), no. 1, 47–70.CrossRefGoogle Scholar
Carlsen, T. and Eilers, S., Matsumoto $K$ -groups associated to certain shift spaces . Doc. Math. 9(2004), 639–671.CrossRefGoogle Scholar
Carlsen, T. and Matsumoto, K., Some remarks on the  ${C}^{\ast }$ -algebras associated with subshifts . Math. Scand. 95(2004), no. 1, 145–160.CrossRefGoogle Scholar
Cassaigne, J. and Karhumäki, J., Toeplitz words, generalized periodicity and periodically iterated morphisms . European J. Combin. 18(1997), 497–510.CrossRefGoogle Scholar
Cuntz, J. and Krieger, W., A class of  ${C}^{\ast }$ -algebras and topological Markov chains . Invent. Math. 56(1980), no. 3, 251–268.CrossRefGoogle Scholar
Guentner, E., Willett, R., and Yu, G., Dynamic asymptotic dimension: relation to dynamics, topology, coarse geometry, and  ${C}^{\ast }$ -algebras . Math. Ann. 367(2017), nos. 1–2, 785–829.CrossRefGoogle Scholar
Katayama, Y., Matsumoto, K., and Watatani, Y., Simple  ${C}^{\ast }$ -algebras arising from  $\beta$ -expansion of real numbers . Ergodic Theory Dynam. Systems 18(1998), no. 4, 937–962.CrossRefGoogle Scholar
Krieger, W. and Matsumoto, K., Shannon graphs, subshifts and lambda-graph systems . J. Math. Soc. Japan 54(2002), 877–899.CrossRefGoogle Scholar
Lin, H. and Su, H., Classification of direct limits of generalized Toeplitz algebras . Pacific J. Math. 181(1997), 89–140.CrossRefGoogle Scholar
Matsumoto, K., $K$ -theory for  ${C}^{\ast }$ -algebras associated with subshifts . Math. Scand. 82(1998), no. 2, 237–255.CrossRefGoogle Scholar
Matsumoto, K., Relations among generators of  ${C}^{\ast }$ -algebras associated with subshifts . Internat. J. Math. 10(1999), no. 3, 385–405.CrossRefGoogle Scholar
Matsumoto, K., Stabilized  ${C}^{\ast }$ -algebras constructed from symbolic dynamical systems . Ergodic Theory Dynam. Systems 20(2000), no. 3, 821–841.CrossRefGoogle Scholar
Parry, W., Symbolic dynamics and transformations of the unit interval . Trans. Amer. Math. Soc. 122(1966), 368–378.CrossRefGoogle Scholar
Sims, A. and Williams, D., The primitive ideals of some étale groupoid  ${C}^{\ast }$ -algebras . Algebr. Represent. Theory 19(2016), no. 2, 255–276.CrossRefGoogle Scholar
Williams, S., Toeplitz minimal flows which are not uniquely ergodic . Z. Wahrsch. Verw. Gebiete. 67(1984), 95–107.CrossRefGoogle Scholar
Winter, W. and Zacharias, J., The nuclear dimension of  ${C}^{\ast }$ -algebras . Adv. Math. 224(2010), no. 2, 461–498.CrossRefGoogle Scholar