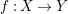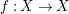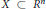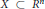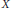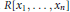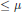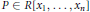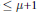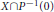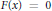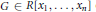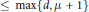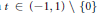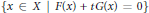We propose a version of the classical Artin approximation that allows us to perturb the variables of the approximated solution. Namely, it is possible to approximate a formal solution of a Nash equation by a Nash solution in a compatible way with a given Nash change of variables. This result is closely related to the so-called nested Artin approximation and becomes false in the analytic setting. We provide local and global versions of this approximation in real and complex geometry together with an application to the Right-Left equivalence of Nash maps.

A semialgebraic map f:X\rightarrow Y$f:X\rightarrow Y$ between two real algebraic sets is called blow-Nash if it can be made Nash (i.e., semialgebraic and real analytic) by composing with finitely many blowings-up with nonsingular centers.

We prove that if a blow-Nash self-homeomorphism f:X\rightarrow X$f:X\rightarrow X$ satisfies a lower bound of the Jacobian determinant condition then f^{-1}$f^{-1}$ is also blow-Nash and satisfies the same condition.

The proof relies on motivic integration arguments and on the virtual Poincaré polynomial of McCrory–Parusiński and Fichou. In particular, we need to generalize Denef–Loeser change of variables key lemma to maps that are generically one-to-one and not merely birational.

To any Nash germ invariant under right composition with a linear action of a finite group, we associate its equivariant zeta functions, inspired from motivic zeta functions, using the equivariant virtual Poincaré series as a motivic measure. We show Denef–Loeser formulas for the equivariant zeta functions and prove that they are invariants for equivariant blow-Nash equivalence via equivariant blow-Nash isomorphisms. Equivariant blow-Nash equivalence between invariant Nash germs is defined as a generalization involving equivariant data of the blow-Nash equivalence.

Let R$R$ be a real closed field, let 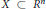X\,\subset \,{{R}^{n}}$X\,\subset \,{{R}^{n}}$ be an irreducible real algebraic set and let 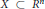Z$Z$ be an algebraic subset of 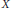X$X$ of codimension ≥ 2. Dubois and Efroymson proved the existence of an irreducible algebraic subset of 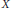X$X$ of codimension 1 containing 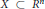Z$Z$. We improve this dimension theorem as follows. Indicate by \mu$\mu$ the minimum integer such that the ideal of polynomials in 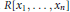R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$ vanishing on 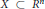Z$Z$ can be generated by polynomials of degree 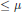\le \,\mu$\le \,\mu$. We prove the following two results: (1) There exists a polynomial 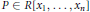P\,\in \,R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$P\,\in \,R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$ of degree 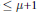\le \,\mu +1$\le \,\mu +1$ such that 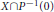X\cap {{P}^{-1}}\left( 0 \right)$X\cap {{P}^{-1}}\left( 0 \right)$ is an irreducible algebraic subset of 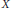X$X$ of codimension 1 containing 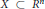Z$Z$. (2) Let F$F$ be a polynomial in 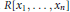R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$ of degree d$d$ vanishing on 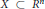Z$Z$. 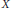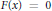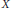Suppose there exists a nonsingular point x$x$ of X$X$ such that F\left( x \right)\,=\,0$F\left( x \right)\,=\,0$ and the differential at x$x$ of the restriction of F$F$ to X$X$ is nonzero. Then there exists a polynomial 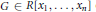G\,\in \,R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$G\,\in \,R\left[ {{x}_{1}}\,,\,.\,.\,.\,,\,{{x}_{n}} \right]$ of degree 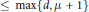\le \,\max \{d,\,\mu \,+\,1\}$\le \,\max \{d,\,\mu \,+\,1\}$ such that, for each 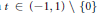t\,\in \,\left( -1,\,1 \right)\,\backslash \,\{0\}$t\,\in \,\left( -1,\,1 \right)\,\backslash \,\{0\}$, the set 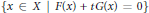\{x\in X|F\left( x \right)+tG\left( x \right)=0\}$\{x\in X|F\left( x \right)+tG\left( x \right)=0\}$ is an irreducible algebraic subset of 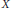X$X$ of codimension 1 containing 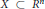Z$Z$. Result (1) and a slightly different version of result (2) are valid over any algebraically closed field also.

We define invariants of the blow-Nash equivalence of Nash function germs, in a similar way to the motivic zeta functions of Denef and Loeser. As a key ingredient, we extend the virtual Betti numbers, which were known for real algebraic sets, to a generalized Euler characteristic for projective constructible arc-symmetric sets. Actually we prove more: the virtual Betti numbers are not only algebraic invariants, but also Nash invariants of arc-symmetric sets. Our zeta functions enable one to distinguish the blow-Nash equivalence classes of Brieskorn polynomials of two variables. We prove moreover that there are no moduli for the blow-Nash equivalence in the case of an algebraic family with isolated singularities.