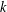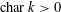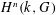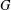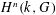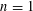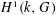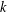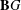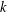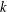Arithmetic duality theorems over a local field 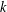$k$ are delicate to prove if 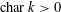$\text{char}\,k>0$. In this case, the proofs often exploit topologies carried by the cohomology groups 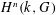$H^{n}(k,G)$ for commutative finite type 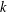$k$-group schemes 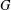$G$. These ‘Čech topologies’, defined using Čech cohomology, are impractical due to the lack of proofs of their basic properties, such as continuity of connecting maps in long exact sequences. We propose another way to topologize 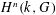$H^{n}(k,G)$: in the key case when 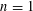$n=1$, identify 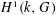$H^{1}(k,G)$ with the set of isomorphism classes of objects of the groupoid of 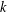$k$-points of the classifying stack 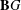$\mathbf{B}G$ and invoke Moret-Bailly’s general method of topologizing 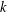$k$-points of locally of finite type 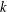$k$-algebraic stacks. Geometric arguments prove that these ‘classifying stack topologies’ enjoy the properties expected from the Čech topologies. With this as the key input, we prove that the Čech and the classifying stack topologies actually agree. The expected properties of the Čech topologies follow, and these properties streamline a number of arithmetic duality proofs given elsewhere.

The well-known fiber dimension theorem in algebraic geometry says that for every morphism f:X→Y of integral schemes of finite type the dimension of every fiber of f is at least dim X−dim Y. This has recently been generalized by Brosnan, Reichstein and Vistoli to certain morphisms of algebraic stacks f:𝒳→𝒴, where the usual dimension is replaced by essential dimension. We will prove a general version for morphisms of categories fibered in groupoids. Moreover, we will prove a variant of this theorem, where essential dimension and canonical dimension are linked. These results let us relate essential dimension to canonical dimension of algebraic groups. In particular, using the recent computation of the essential dimension of algebraic tori by MacDonald, Meyer, Reichstein and the author, we establish a lower bound on the canonical dimension of algebraic tori.

Lie algebroids cannot always be integrated into Lie groupoids. We introduce a new structure, ‘Weinstein groupoid’, which may be viewed as stacky groupoids. We use this structure to present a solution to the integration problem of Lie algebroids. It turns out that every Weinstein groupoid has a Lie algebroid and every Lie algebroid can be integrated into such a groupoid.