2 results
Alternative polarizations of Borel fixed ideals
-
- Journal:
- Nagoya Mathematical Journal / Volume 207 / September 2012
- Published online by Cambridge University Press:
- 11 January 2016, pp. 79-93
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Numerical-symbolic exact irreducible decomposition of cyclic-12
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 155-172
-
- Article
-
- You have access
- Export citation

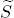 such that
such that 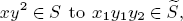 ours sends it to
ours sends it to 