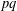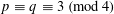Search

BIG BIASES AMONGST PRODUCTS OF TWO PRIMES
Part of
- Exponential sums and character sums
- Multiplicative number theory
David Dummit, Andrew Granville, Hershy Kisilevsky
Journal:

Mathematika / Volume 62 / Issue 2 / 2016

Published online by Cambridge University Press:

18 February 2016, pp. 502-507

Print publication:

2016
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
We show that substantially more than a quarter of the odd integers of the form $pq$ up to $x$, with $p,q$ both prime, satisfy $p\equiv q\equiv 3~(\text{mod}\,4)$.

PRIMES IN BEATTY SEQUENCES IN SHORT INTERVALS
Part of
- Multiplicative number theory
Glyn Harman
Journal:

Mathematika / Volume 62 / Issue 2 / 2016

Published online by Cambridge University Press:

17 February 2016, pp. 572-586

Print publication:

2016
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
In this paper we show that sieve methods used previously to investigate primes in short intervals and corresponding Goldbach-type problems can be modified to obtain results on primes in Beatty sequences in short intervals.

Pretentious multiplicative functions and the prime number theorem for arithmetic progressions
Part of
- Multiplicative number theory
- Zeta and $L$-functions: analytic theory
Dimitris Koukoulopoulos
Journal:

Compositio Mathematica / Volume 149 / Issue 7 / July 2013

Published online by Cambridge University Press:

14 May 2013, pp. 1129-1149

Print publication:

July 2013
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
Building on the concept of pretentious multiplicative functions, we give a new and largely elementary proof of the best result known on the counting function of primes in arithmetic progressions.

on the number of carmichael numbers up to $\lowercase{x}$
glyn harman
Journal:

Bulletin of the London Mathematical Society / Volume 37 / Issue 5 / October 2005

Published online by Cambridge University Press:

23 September 2005, pp. 641-650

Print publication:

October 2005
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
it is shown that, for all large $x$, there are more than $x^{0.33}$ carmichael numbers up to $x$, improving on the ground-breaking work of alford, granville and pomerance, who were the first to demonstrate that there are infinitely many such numbers. the same basic construction as that employed by these authors is used, but a slight modification enables a stronger result on primes in arithmetic progressions based on a sieve method to be employed.

Search Results