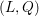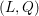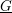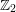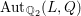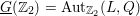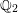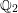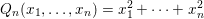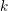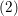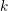The celebrated Smith–Minkowski–Siegel mass formula expresses the mass of a quadratic lattice 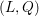(L,Q)$(L,Q)$ as a product of local factors, called the local densities of 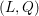(L,Q)$(L,Q)$. This mass formula is an essential tool for the classification of integral quadratic lattices. In this paper, we will describe the local density formula explicitly by observing the existence of a smooth affine group scheme 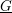\underline{G}$\underline{G}$ over 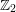\mathbb{Z}_{2}$\mathbb{Z}_{2}$ with generic fiber 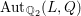\text{Aut}_{\mathbb{Q}_{2}}(L,Q)$\text{Aut}_{\mathbb{Q}_{2}}(L,Q)$, which satisfies 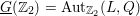\underline{G}(\mathbb{Z}_{2})=\text{Aut}_{\mathbb{Z}_{2}}(L,Q)$\underline{G}(\mathbb{Z}_{2})=\text{Aut}_{\mathbb{Z}_{2}}(L,Q)$. Our method works for any unramified finite extension of 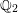\mathbb{Q}_{2}$\mathbb{Q}_{2}$. Therefore, we give a long awaited proof for the local density formula of Conway and Sloane and discover its generalization to unramified finite extensions of 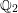\mathbb{Q}_{2}$\mathbb{Q}_{2}$. As an example, we give the mass formula for the integral quadratic form 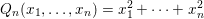Q_{n}(x_{1},\dots ,x_{n})=x_{1}^{2}+\cdots +x_{n}^{2}$Q_{n}(x_{1},\dots ,x_{n})=x_{1}^{2}+\cdots +x_{n}^{2}$ associated to a number field 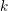k$k$ which is totally real and such that the ideal 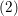(2)$(2)$ is unramified over 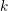k$k$.

If a positive definite Hermitian lattice represents all positive integers, we call it universal. Several mathematicians, including the author, have between them found 25 universal binary Hermitian lattices. But their ad hoc proofs are complicated. We give simple and unified proofs of universality.

J. S. Hsia has conjectured an arithmetical version of Springer Theorem, which states that no two spinor genera in the same genus of integral quadratic forms become identified over an odd degree extension. In this paper we prove by examples that the corresponding result for quaternionic skew-hermitian forms does not hold in full generality. We prove that it does hold for unimodular skew-hermitian lattices under all extensions and for lattices whose discriminant is relatively prime to 2 under Galois extensions.