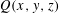3 results
SMALL SOLUTIONS OF QUADRATIC CONGRUENCES, AND CHARACTER SUMS WITH BINARY QUADRATIC FORMS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 18 February 2016, pp. 551-571
- Print publication:
- 2016
-
- Article
- Export citation
Ternary quadratic forms and half-integral weight modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 December 2012, pp. 418-435
-
- Article
-
- You have access
- Export citation
DISCRIMINANT BOUNDS FOR SPINOR REGULAR TERNARY QUADRATIC LATTICES
-
- Journal:
- Journal of the London Mathematical Society / Volume 69 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 24 May 2004, pp. 545-561
- Print publication:
- June 2004
-
- Article
- Export citation