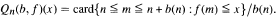For given multiplicative function 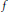 $f$, with
$f$, with 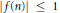 $\left| f\left( n \right) \right|\le 1$ for all
$\left| f\left( n \right) \right|\le 1$ for all  $n$, we are interested in how fast its mean value
$n$, we are interested in how fast its mean value 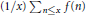 $\left( 1/x \right)\sum{_{n\le x}f\left( n \right)}$ converges. Halász showed that this depends on the minimum
$\left( 1/x \right)\sum{_{n\le x}f\left( n \right)}$ converges. Halász showed that this depends on the minimum 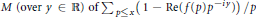 $M\,\left( \text{over}\,y\,\in \,\mathbb{R} \right)\,\text{of}\,\sum{_{p\le x}\left( 1-\operatorname{Re}\left( f\left( p \right){{p}^{-iy}} \right) \right)}/p$, and subsequent authors gave the upper bound
$M\,\left( \text{over}\,y\,\in \,\mathbb{R} \right)\,\text{of}\,\sum{_{p\le x}\left( 1-\operatorname{Re}\left( f\left( p \right){{p}^{-iy}} \right) \right)}/p$, and subsequent authors gave the upper bound 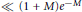 $\ll \left( 1+M \right){{e}^{-M}}$. For many applications it is necessary to have explicit constants in this and various related bounds, and we provide these via our own variant of the Halász-Montgomery lemma (in fact the constant we give is best possible up to a factor of 10). We also develop a new type of hybrid bound in terms of the location of the absolute value of
$\ll \left( 1+M \right){{e}^{-M}}$. For many applications it is necessary to have explicit constants in this and various related bounds, and we provide these via our own variant of the Halász-Montgomery lemma (in fact the constant we give is best possible up to a factor of 10). We also develop a new type of hybrid bound in terms of the location of the absolute value of  $y$ that minimizes the sum above. As one application we give bounds for the least representatives of the cosets of the
$y$ that minimizes the sum above. As one application we give bounds for the least representatives of the cosets of the  $k$-th powers mod
$k$-th powers mod 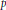 $p$.
$p$.

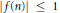

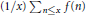
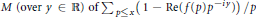
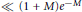


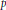
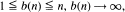 let
let