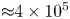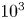Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T14:37:30.521Z Has data issue: false hasContentIssue false
  • English
  • Français

A measurement of the effective mean free path of solar wind protons

Part of: Featured Articles

Published online by Cambridge University Press:  19 September 2022

Jesse T. Coburn Open the ORCID record for Jesse T. Coburn [Opens in a new window] ,
Christopher H.K. Chen Open the ORCID record for Christopher H.K. Chen [Opens in a new window]  and
Jonathan Squire Open the ORCID record for Jonathan Squire [Opens in a new window]
Jesse T. Coburn*
Affiliation:
Department of Physics and Astronomy, Queen Mary University of London, London E1 4NS, UK
Christopher H.K. Chen
Affiliation:
Department of Physics and Astronomy, Queen Mary University of London, London E1 4NS, UK
Jonathan Squire
Affiliation:
Physics Department, University of Otago, Dunedin 9010, New Zealand
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Weakly collisional plasmas are subject to nonlinear relaxation processes, which can operate at rates much faster than the particle collision frequencies. This causes the plasma to respond like a magnetised fluid despite having long particle mean free paths. In this Letter the effective collisional mechanisms are modelled in the plasma kinetic equation to produce density, pressure and magnetic-field responses to compare with spacecraft measurements of the solar wind compressive fluctuations at 1 AU. This enables a measurement of the effective mean free path of the solar wind protons, found to be ${\approx }4 \times 10^{5}$ km, which is approximately $10^{3}$ times shorter than the collisional mean free path. These measurements are shown to support the effective fluid behaviour of the solar wind at scales above the proton gyroradius and demonstrate that effective collision processes alter the thermodynamics and transport of weakly collisional plasmas.

Keywords

space plasma physicsplasma properties
Type
Letter
Information
Journal of Plasma Physics , Volume 88 , Issue 5 , October 2022 , 175880502
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution and reproduction, provided the original article is properly cited.
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press

1. Introduction

Many natural plasmas (e.g. interstellar medium, galaxy clusters, black hole accretion disks, solar wind) are in a weakly collisional state, where the particle collision frequency $\nu _{\mathrm {coll}}$ is smaller than other characteristic frequencies (e.g. proton gyrofrequency $\varOmega _{\mathrm {p}}$, inverse magnetic-field correlation time $1/\tau _c$ etc. (Quataert Reference Quataert2003; Marsch Reference Marsch2006; Schekochihin & Cowley Reference Schekochihin and Cowley2006; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). Thus, the regimes of the plasma motions, characterised by $\omega$, can span from collisional (fluid) $\omega \ll \nu _{\mathrm {coll}}$ to collisionless $\omega \gg \nu _{\mathrm {coll}}$, where $\omega$ is the temporal frequency of a fluctuating plasma property (Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005, Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). Knowledge of the transition scale $\omega \sim \nu _{\mathrm {coll}}$ is vital to understand the behaviour of astrophysical plasmas.

The escaping solar corona, known as the solar wind, expands into interplanetary space as a super-Alfvénic and turbulent plasma (Parker Reference Parker1958; Bruno & Carbone Reference Bruno and Carbone2013; Verscharen, Klein & Maruca Reference Verscharen, Klein and Maruca2019). In situ measurements of particle distribution functions and electromagnetic fields enable fundamental plasma physics observations (Chen Reference Chen2016). The Spitzer–Härm proton–proton collision frequency $\nu _{\mathrm {p},\mathrm {p}}^{\mathrm {SH}}$ decreases with radial distance from the Sun and, by a few solar radii, is much smaller than other characteristic frequencies. In principle, the dynamics should be described by collisionless plasma equations. For reference, at 1 AU, typical frequencies are $\nu _{\mathrm {p},\mathrm {p}}^{\mathrm {SH}} \approx 4 \times 10^{-7} \ \mathrm {s}^{-1}$, $\varOmega _{\mathrm {p}} \approx 10^{-1} \ \mathrm {s}^{-1}$, $1/\tau _c \approx 10^{-6} \ \mathrm {s}^{-1}$ (see Appendix A for the calculation of the collision frequency; Spitzer Reference Spitzer1962; Huba Reference Huba1983; Matthaeus et al. Reference Matthaeus, Dasso, Weygand, Kivelson and Osman2010; Verscharen et al. Reference Verscharen, Klein and Maruca2019).

Despite the weak collisionality of the solar wind, many aspects appear to be described by fluid equations: magnetohydrodynamic (MHD) turbulence theory predicts the shape of power spectra (e.g. magnetic field, proton density; Coleman Reference Coleman1968; Matthaeus & Goldstein Reference Matthaeus and Goldstein1982; Tu & Marsch Reference Tu and Marsch1995; Goldreich & Sridhar Reference Goldreich and Sridhar1997; Bruno & Carbone Reference Bruno and Carbone2013), spatial transport (Zank, Matthaeus & Smith Reference Zank, Matthaeus and Smith1996; Matthaeus et al. Reference Matthaeus, Zank, Smith and Oughton1999) and the proton heating rate by the energy cascade (MacBride, Smith & Forman Reference MacBride, Smith and Forman2008; Stawarz et al. Reference Stawarz, Smith, Vasquez, Forman and MacBride2009; Coburn et al. Reference Coburn, Smith, Vasquez, Stawarz and Forman2012). This success is certainly due, in part, to the dominance of Alfvénic fluctuations, which have identical properties in the collisionless and fluid limits on scales above the proton gyroradius, implying much of the turbulent energy cascade is basically insensitive to the plasma's collisionality (Kulsrud, Sagdeev & Rosenbluth Reference Kulsrud, Sagdeev and Rosenbluth1980; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). However, observations show a strong correlation between the density and thermal pressure (i.e. compressive fluctuations), indicating a polytropic equation of state (Marsch et al. Reference Marsch, Muehlhaeuser, Rosenbauer and Schwenn1983; Totten, Freeman & Arya Reference Totten, Freeman and Arya1995; Verscharen, Chen & Wicks Reference Verscharen, Chen and Wicks2017; Nicolaou et al. Reference Nicolaou, Livadiotis, Wicks, Verscharen and Maruca2020). Moreover, compressive fluctuations generally display the MHD slow-mode polarisation (anticorrelated magnetic and thermal pressure; Verscharen et al. Reference Verscharen, Chen and Wicks2017), rather than being severely damped, as expected in a collisionless plasma (Barnes Reference Barnes1966). These modes are routinely detected at a range of scales (Tu & Marsch Reference Tu and Marsch1995; Kellogg & Horbury Reference Kellogg and Horbury2005; Yao et al. Reference Yao, He, Marsch, Tu, Pedersen, Rème and Trotignon2011; Howes et al. Reference Howes, Bale, Klein, Chen, Salem and TenBarge2012; Klein et al. Reference Klein, Howes, TenBarge, Bale, Chen and Salem2012; Yao et al. Reference Yao, He, Tu, Wang and Marsch2013a,Reference Yao, He, Tu, Wang and Marschb) following a power law predicted from the MHD equations (Montgomery, Brown & Matthaeus Reference Montgomery, Brown and Matthaeus1987; Marsch & Tu Reference Marsch and Tu1990; Lithwick & Goldreich Reference Lithwick and Goldreich2001; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009).

While the Spitzer–Härm collision frequency appears incompatible with the fluid-like behaviour of the solar wind, weakly collisional plasmas are also subject to collisionless relaxation processes that prevent extreme departure from equilibrium (Nishida Reference Nishida1969; Griffel & Davis Reference Griffel and Davis1969; Hamasaki & Krall Reference Hamasaki and Krall1973; Gary, Yin & Winske Reference Gary, Yin and Winske2000; Yoon Reference Yoon2017). Solar wind observations present substantial evidence of temperature anisotropy instabilities constraining the particle distribution functions (Kasper, Lazarus & Gary Reference Kasper, Lazarus and Gary2002; Tu & Marsch Reference Tu and Marsch2002; Marsch Reference Marsch2006; Hellinger et al. Reference Hellinger, Trávníček, Kasper and Lazarus2006; Bale et al. Reference Bale, Kasper, Howes, Quataert, Salem and Sundkvist2009; Chen et al. Reference Chen, Matteini, Schekochihin, Stevens, Salem, Maruca, Kunz and Bale2016; Yoon Reference Yoon2017). These processes can play a similar role to collisions viz., they are effective collision processes.

This Letter presents a measurement of the effective mean free path of the solar wind by comparing observations of compressive wave-mode polarisation with numerical solutions of varying effective collision frequency. It is shown that the transition from fluid to collisionless dynamics in the solar wind occurs at scales several orders of magnitude below the classical Spitzer–Härm mean free path, explaining the fluid-like behaviour of the weakly collisional solar wind.

2. Theory and numerical solutions

The kinetic MHD equations with the Bhatnagar–Gross–Krook (BGK) collision operator (Bhatnagar, Gross & Krook Reference Bhatnagar, Gross and Krook1954; Gross & Krook Reference Gross and Krook1956) produce dispersion relations and plasma fluctuations (e.g. magnetic field and pressure) that span between the collisionless and collisional limits (Kulsrud et al. Reference Kulsrud, Sagdeev and Rosenbluth1980; Snyder, Hammett & Dorland Reference Snyder, Hammett and Dorland1997; Sharma, Hammett & Quataert Reference Sharma, Hammett and Quataert2003; Chandran et al. Reference Chandran, Dennis, Quataert and Bale2011). They describe a non-relativistic, magnetised plasma of arbitrary collision frequency (Kulsrud et al. Reference Kulsrud, Sagdeev and Rosenbluth1980; Sharma et al. Reference Sharma, Hammett and Quataert2003). See Appendix B for details on the equations and BGK collision operator. The specific equations, which we refer to as kinetic MHD-BGK (KMHD-BGK), model both the proton and electron responses with the kinetic equation so that Landau and Barnes dampings are retained. The BGK operator is used here to model relaxation processes, not particle collisions, so we use the language of an effective proton collision frequency $\nu _{\mathrm {eff}}$ or mean free path $\lambda _{\mathrm {mfp}}^{\mathrm {eff}} = v_{\mathrm {th}}^{\mathrm {p}} / \nu _{\mathrm {eff}}$, where the proton thermal speed is $v_{\mathrm {th}}^{\mathrm {p}}$.

Assuming plasma motions are slow compared with the gyrofrequency $\varOmega _p$, the second moment of the kinetic equation and the ideal induction equation leads to

(2.1a)\begin{gather} n_{\mathrm{p}} B \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{p_{{\perp}}^{\mathrm{p}}}{n_{\mathrm{p}} B} \right) ={-} \boldsymbol{\nabla} \boldsymbol{\cdot} ( q^{\mathrm{p}}_{{\perp}} \hat{\boldsymbol{b}}) - q^{\mathrm{p}}_{{\perp}} \boldsymbol{\nabla} \boldsymbol{\cdot} \hat{\boldsymbol{b}} + \frac{\nu_{\mathrm{eff}}}{3} (p_{{\parallel}}^{\mathrm{p}} - p_{{\perp}}^{\mathrm{p}}), \end{gather}
(2.1b)\begin{gather}\frac{n_{\mathrm{p}}^{3}}{2 B} \frac{\mathrm{d}}{\mathrm{d}t} \left(\frac{p_{{\parallel}}^{\mathrm{p}} B^{2}}{n_{\mathrm{p}}^{3}} \right) ={-} \boldsymbol{\nabla} \boldsymbol{\cdot} (q_{{\parallel}}^{\mathrm{p}} \hat{\boldsymbol{b}} ) + q_{{\perp}}^{\mathrm{p}} \boldsymbol{\nabla} \boldsymbol{\cdot} \hat{\boldsymbol{b}} + \frac{2 \nu_{\mathrm{eff}} }{3} ( p_{{\perp}}^{\mathrm{p}} - p_{{\parallel}}^{\mathrm{p}} ), \end{gather}

where $\mathrm {d}/\mathrm {d}t$ is the convective derivative and the quantities are the proton density $n_{\mathrm {p}}$, magnetic-field strength $B$, parallel (perpendicular) proton pressure $p_{\parallel }^{\mathrm {p}} \ (p_{\perp }^{\mathrm {p}})$, field parallel flux of parallel (perpendicular) proton heat $q_{\parallel }^{\mathrm {p}} \ (q_{\perp }^{\mathrm {p}})$ and the unit magnetic-field vector $\hat {\boldsymbol {b}} = \boldsymbol {B} / B$ (Chew, Goldberger & Low Reference Chew, Goldberger and Low1956; Hunana et al. Reference Hunana, Tenerani, Zank, Khomenko, Goldstein, Webb, Cally, Collados, Velli and Adhikari2019). The Alfvén speed is $v_A= B/\sqrt {4 {\rm \pi}n_{\mathrm {p}} m_{\mathrm {p}}}$, the proton gyroradius is $\rho _{\mathrm {p}} = v_{\mathrm {th}}^{\mathrm {p}} / \varOmega _{\mathrm {p}}$ and the ion-acoustic speed is $c_{\mathrm {s}} = \sqrt {(3 k_{\mathrm {B}} T_{\parallel }^{\mathrm {p}} + k_{\mathrm {B}} T_{\parallel }^{\mathrm {e}})/m_{\mathrm {p}}}$, where the parallel proton (electron) temperature is $T_{\parallel }^{\mathrm {p}} (T_{\parallel }^{\mathrm {e}})$.

Equations (2.1) are often discussed when the right-hand sides are zero and are then referred to as the double adiabatic equations or Chew–Goldberger–Low (CGL) invariants (Chew et al. Reference Chew, Goldberger and Low1956). The focus here is on how the CGL invariants are broken, for example, by the heat flux terms in the collisionless limit, and by the effective collisional terms ($\propto \nu _{\mathrm {eff}}$). Therefore, the relative non-conservation of the CGL invariants provides a sensitive test of the equation of state.

Cross-correlations and amplitude ratios, which can be measured, are constructed from the left-hand sides of (2.1),

(2.2a)\begin{gather} C_{{\parallel}} = \frac{ \langle \delta p_{{\parallel}}^{\mathrm{p}}\, \delta (n^{3}_{\mathrm{p}} / B^{2}) \rangle }{ \langle | \delta p_{{\parallel}}^{\mathrm{p}} |^{2} \rangle^{1/2} \langle | \delta (n^{3}_{\mathrm{p}} / B^{2}) |^{2} \rangle^{1/2}} , \end{gather}
(2.2b)\begin{gather}A_{{\parallel}} =\frac{ \langle | \delta (n^{3}_{\mathrm{p}}/ B^{2}) |^{2} \rangle^{1/2} }{ \langle n^{3}_{\mathrm{p}}/ B^{2} \rangle } \frac{ \langle p_{{\parallel}}^{\mathrm{p}} \rangle }{ \langle | \delta p_{{\parallel}}^{\mathrm{p}} |^{2} \rangle^{1/2} } , \end{gather}
(2.2c)\begin{gather}C_{{\perp}} = \frac{ \langle \delta p_{{\perp}}^{\mathrm{p}} \, \delta (n_{\mathrm{p}} B) \rangle }{ \langle | \delta p_{{\perp}}^{\mathrm{p}} |^{2} \rangle^{1/2} \langle | \delta (n_{\mathrm{p}} B) |^{2} \rangle^{1/2}} , \end{gather}
(2.2d)\begin{gather}A_{{\perp}} = \frac{ \langle | \delta (n_{\mathrm{p}} B) |^{2} \rangle^{1/2} }{ \langle n_{\mathrm{p}} B \rangle } \frac{ \langle p_{{\perp}}^{\mathrm{p}} \rangle }{ \langle | \delta p_{{\perp}}^{\mathrm{p}} |^{2} \rangle^{1/2} } , \end{gather}

where $\delta \chi = \chi - \langle \chi \rangle$ is the fluctuation about the average $\langle \chi \rangle$. They describe the relative non-conservation of the CGL invariants. The method compares predictions for (2.2) derived from the slow-mode eigenmodes of the linearised KMHD-BGK system (e.g. $\delta p_{\perp }^{\mathrm {p}}, \, \delta B$ etc.) with solar wind measurements, since the slow mode is the dominant compressive mode at large scales (Howes et al. Reference Howes, Bale, Klein, Chen, Salem and TenBarge2012). A description of the equations and the linear system of equations appears in Appendix B.

The model's free parameters are the propagation angle $\theta _{\hat {\boldsymbol {b}},\hat {\boldsymbol {k}}}$ and proton effective mean free path $\lambda _{\mathrm {mfp}}^{\mathrm {eff}}$; they are determined by fitting to solar wind observations. The wavenumber $k$ and the proton beta $\beta = 8 {\rm \pi}p^{\mathrm {p}} / B^{2}$, where $p^{\mathrm {p}} = 2p^{\mathrm {p}}_{\perp }/3 + p^{\mathrm {p}}_{\parallel }/3$, are set to measured values. The species temperature ratio is set to a typical value for the solar wind $T_{\mathrm {p}} / T_{\mathrm {e}} = 1$ and the effective mean free path species ratio is set to $\lambda _{\mathrm {mfp}}^{\mathrm {eff}} / \lambda _{\mathrm {mfp,electrons}}^{\mathrm {eff}} = 1$ (see Appendix B for details). At small $\beta$, these two ratios $T_{\mathrm {p}} / T_{\mathrm {e}}, \, \lambda _{\mathrm {mfp}}^{\mathrm {eff}} / \lambda _{\mathrm {mfp,electrons}}^{\mathrm {eff}}$ have an insignificant influence on the correlations, (2.2), and nearly no influence at large $\beta$.

Figure 1 demonstrates the ability of the KMHD-BGK equations to resolve the dynamics of the compressive slow mode from collisional (lighter blue) to collisionless (black). Numerical predictions for (2.2a), (2.2c) (bottom panels of figure 1) show distinct differences at $\beta > 1$ for different $k_{\parallel } \lambda _{\mathrm {mfp}}^{\mathrm {eff}}$, which can be compared with observations. The MHD ($k_{\parallel } \lambda _{\mathrm {mfp}}^{\mathrm {eff}} \ll 1$) and collisionless ($k_{\parallel } \lambda _{\mathrm {mfp}}^{\mathrm {eff}} \gg 1$) limits are illustrated in magenta, for $C_{\perp }$ (bottom right panel) these two limits produce similar trends, therefore it is necessary to make comparisons at multiple $k_{\parallel }$ to measure $\lambda _{\mathrm {mfp}}^{\mathrm {eff}}$.

Figure 1. Numerical solutions of the KMHD-BGK equations for a range of $k_{\parallel } \lambda _{\mathrm {mfp}}^{\mathrm {eff}}$ (see colour bar). The imaginary (real) part of the complex frequency is denoted $\gamma \ (\omega _r)$. The dotted (dashed) magenta lines are the long (short) limit of $\lambda _{\mathrm {mfp}}^{\mathrm {eff}}$ corresponding to the collisionless (collisional) slow-mode/ion-acoustic branch for $\theta _{\hat {\boldsymbol {b}},\hat {\boldsymbol {k}}} = 88^{\circ }$ (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Verscharen et al. Reference Verscharen, Chen and Wicks2017).

3. Measurements

The dataset consists of Wind spacecraft measurements of the pristine solar wind during years 2005–2010. The electrostatic analyser, 3DP, records onboard moments of the proton density, velocity and pressure tensor, and the magnetometer MFI records the magnetic field, at a nominal ${\sim }3s$ cadence (Lepping et al. Reference Lepping, Acũna, Burlaga, Farrell, Slavin, Schatten, Mariani, Ness, Neubauer and Whang1995; Lin et al. Reference Lin, Anderson, Ashford, Carlson, Curtis, Ergun, Larson, McFadden, McCarthy and Parks1995).

The dataset is restricted to time intervals satisfying three criteria: (i) 95 % of the data are available (the remaining are then linearly interpolated); (ii) the median density must be greater than 1 particle per cm$^{3}$; and (iii) the average norm of the non-gyrotropic tensor ($\mathit{\boldsymbol{\Pi}} ^{\mathrm {p}} =\boldsymbol{ \mathsf{ p}}^{\mathrm {p}} - \hat {\boldsymbol {b}} \hat {\boldsymbol {b}} \, p^{\mathrm {p}}_{\parallel } - (1 - \hat {\boldsymbol {b}} \hat {\boldsymbol {b}} ) p_{\perp }^{\mathrm {p}}$), must be less than 30 % of the average norm of the pressure tensor $\boldsymbol{ \mathsf{ p}}^{\mathrm {p}}$. The final point here is satisfied $\sim$94 % of the time at the ${\sim }3s$ time interval and more so at longer time intervals.

To probe a set of wavenumbers, the four quantities in (2.2) are measured, along with the average radial solar wind velocity $\langle V_{\mathrm {SW}} \rangle$ and the average proton beta for a set of time intervals $\tau = [30\ \mathrm {s}, 1\ \mathrm {min.}, 2\ \mathrm {mins.}, \ldots, 128\ \mathrm {mins.}]$. The time scales are converted to wavenumber $k_{\mathrm {SW}} = 1/ \tau \langle V_{\mathrm {SW}} \rangle$ via Taylor's frozen-in-flow (TFF) assumption (Taylor Reference Taylor1938). Outliers in the distribution of $k_{\mathrm {SW}}$ are removed and then three bins of equal probability density are obtained where the median of each bin is $k_{\mathrm {SW}} = [0.288, 1.41, 6.34] \times 10^{-5} \ \mathrm {km}^{-1}$, which lies within the inertial range of the magnetic-field power spectrum at 1 AU (Kiyani, Osman & Chapman Reference Kiyani, Osman and Chapman2015). The choice of bins provides enough separation in wavenumber to resolve differences in the measured quantities (e.g. figure 1) and sufficient sampling; the wavenumber bins contain $[2.98, 16.6, 70.0] \times 10^{5}$ samples.

For bin $k_{\mathrm {SW}} = 0.288 \times 10^{-5} \ \mathrm {km}^{-1}$ the $\beta$-conditioned probability functions of (2.2), mapped to a common colour bar, are displayed in figure 2. The $\beta$-trend lines in magenta (see caption) capture statistically significant differences between $\beta \lessgtr 1$. From the correlations $C_{\parallel }, C_{\perp }$ it is clear that the CGL invariants are rarely conserved $(C_{\parallel }, C_{\perp } = 1)$, but display similar trends to the theoretical expectations seen in figure 1. The amplitude ratios $A_{\parallel }, A_{\perp }$ demonstrate a relative decrease in fluctuation amplitude of the pressure components at $\beta > 1$.

Figure 2. The $\beta$-conditioned probability functions of the quantities in (2.2) for the wavenumber bin $k_{\mathrm {SW}} = 0.288 \times 10^{-5} \ \mathrm {km}^{-1}$. The thin black line is a contour of probability equal to 0.01. The magenta lines are mean (dashed), median (solid) and maximum (dotted) conditioned on $\beta$.

4. Comparison of measurements and numerical solutions

The theoretical predictions for (2.2) from the numerical model in § 2 are compared with the observations in figure 2 to determine the most probable effective mean free path $\lambda _{\mathrm {mfp}}^{\mathrm {eff}}$ and propagation angles $\theta _{\hat {\boldsymbol {b}},\hat {\boldsymbol {k}}}$. The numerical predictions can be fitted to the observations by altering the parameters (e.g. the effective mean free path), but a degeneracy in parametrisation must be dealt with. The numerical solutions primarily depend on $k_{\parallel } \lambda _{\mathrm {mfp}}^{\mathrm {eff}} = k \cos (\theta _{\hat {\boldsymbol {b}},\hat {\boldsymbol {k}}}) \lambda _{\mathrm {mfp}}^{\mathrm {eff}}$ (Sharma et al. Reference Sharma, Hammett and Quataert2003), which implies that $\lambda _{\mathrm {mfp}}^{\mathrm {eff}}$ and $\theta _{\hat {\boldsymbol {b}},\hat {\boldsymbol {k}}}$ are degenerate. To address this, a scale-dependent anisotropy model $(k_{\parallel } \sim k_{\perp }^{\alpha })$ is introduced, which relates $k$ and $\theta _{\hat {\boldsymbol {b}},\hat {\boldsymbol {k}}}$,

(4.1)\begin{equation} k = \frac{k_{\mathrm{iso}}}{\sqrt{2}} \,\big[ \mathrm{sin} \big( \theta_{\hat{\boldsymbol{b}},\hat{\boldsymbol{k}}} \big) \big]^{\alpha/(1-\alpha)} \,\big[\cos\big(\theta_{\hat{\boldsymbol{b}},\hat{\boldsymbol{k}}} \big) \big]^{1/(\alpha - 1)}, \end{equation}

where $k_{\mathrm {iso}}$ is the isotropic wavenumber ($k = k_{\mathrm {iso}}$ when $k_{\perp } = k_{\parallel }$) and $\alpha$ is the anisotropy exponent, generalised from turbulence models (Goldreich & Sridhar Reference Goldreich and Sridhar1995). The wavenumber model provides $\theta _{\hat {\boldsymbol {b}},\hat {\boldsymbol {k}}}$, given $k$, parameterised by $\alpha, k_{\mathrm {iso}}$, so that $\lambda _{\mathrm {mfp}}^{\mathrm {eff}}$ can be determined at the given wavenumber. Then comparing solutions parameterised by $\lambda _{\mathrm {mfp}}^{\mathrm {eff}}$, $\alpha$, $k_{\mathrm {iso}}$ at multiple wavenumbers $k = k_{\mathrm {SW}}$ clears the degeneracy and allows all three parameters to be measured. Additionally, the model permits quantification of the observed increase of obliqueness with wavenumber of the compressive fluctuations (Chen et al. Reference Chen, Mallet, Schekochihin, Horbury, Wicks and Bale2012; Chen Reference Chen2016).

Finally, the predictions of (2.2) from the numerical solutions are normalised to the measured $\beta$-conditioned mean value (dashed magenta lines in figure 2) of $C_{\parallel }, C_{\perp }, A_{\parallel }, A_{\perp }$ at $\beta \simeq 10^{-1}$. This is to account for the fact that linear wave properties are only approximately observed in strong turbulence (Chen Reference Chen2016; Grošelj et al. Reference Grošelj, Chen, Mallet, Samtaney, Schneider and Jenko2019).

The ranges $\alpha = [0.05,1.0]$, $k_{\mathrm {iso}} = [5 \times 10^{-9}, 5 \times 10^{-7}]\ \mathrm {km}^{-1}$ and $\lambda _{\mathrm {mfp}}^{\mathrm {eff}} = [3.5 \times 10^{4}, 2.1 \times 10^{6}] \ \mathrm {km}$ are chosen for computing numerical solutions. The ranges of $\alpha, k_{\mathrm {iso}}$ are consistent with previous observations (Chen et al. Reference Chen, Mallet, Schekochihin, Horbury, Wicks and Bale2012; Chen Reference Chen2016). The range of $\lambda _{\mathrm {mfp}}^{\mathrm {eff}}$ returns numerical solutions of (2.2) that compare qualitatively well with the observations (seen in figure 2). The Spitzer–Härm mean free path returns the (collisionless) ion-acoustic dispersion relation which is inconsistent with the measurements.

To make a quantitative comparison, we compute the ‘goodness of fit’

(4.2)\begin{equation} R = \sqrt{N^{{-}1} \sum_i^{N} \, (\bar{y}_i - \hat{y}_i)^{2}}, \end{equation}

where $\hat {y}_i$ ($\bar {y}_i$) is the local numerical solution (local measured mean), summed over $i$, denoting the $i$th $\beta$-bin. Here, $R(k_{\mathrm {SW}}; \alpha, k_{\mathrm {iso}}, \lambda _{\mathrm {mfp}}^{\mathrm {eff}})$ is calculated for each wavenumber $k_{\mathrm {SW}}$, where the mean $\bar {y}_i$ is respective to the wavenumber bin. The $R$-values are inverted for unnormalised weights ($w = R^{-1}$), divided by the maximum weight ($w_{\mathrm {max}}$), then summed over wavenumber $\mathcal {W}(\alpha, k_{\mathrm {iso}}, \lambda _{\mathrm {mfp}}^{\mathrm {eff}}) = \sum _k w(k; \alpha, k_{\mathrm {iso}}, \lambda _{\mathrm {mfp}}^{\mathrm {eff}})/ w_{\mathrm {max}}$ to break the aforementioned degeneracy. From this volume, weighted geometric means $\mu _x$, covariances $\sigma ^{2}_{x,y}$, and two sigma confidence intervals $\mathrm {CI}_{x}$ are calculated (see Appendix C for the statistics; Norris Reference Norris1940; Kendall & Stuart Reference Kendall and Stuart1977). This is the method employed to measure the quantities $\lambda _{\mathrm {mfp}}^{\mathrm {eff}}, \alpha, k_{\mathrm {iso}}$, providing the main results of the Letter.

To visualise the weighted parameter space for $C_{\perp }$, figure 3 illustrates the weight volume $\mathcal {W}(\alpha, k_{\mathrm {iso}}, \lambda _{\mathrm {mfp}}^{\mathrm {eff}})$ numerically integrated over each parameter axis $\chi$,

(4.3)\begin{equation} \mathcal{W}_{\chi} = \int_{\chi_0}^{\chi_n} \, {\rm d} \chi \, \frac{\mathcal{W}(\alpha, k_{\mathrm{iso}}, \lambda_{\mathrm{mfp}}^{\mathrm{eff}})}{\chi_n - \chi_0}, \end{equation}

where $\chi _n, \chi _0$ are limits of the range. The weighted means in figure 3 lie in the maximum regions of $\mathcal {W}_{\chi }$, within the confidence intervals, indicating the weighted geometric statistics are a good representation of the observations.

Figure 3. The three panels display the integrated weight volume, (4.3), for each parameter $\chi$, for $C_{\perp }$. The magenta crosses indicate the weighted geometric means and two sigma confidence intervals.

To check the scale dependence, figure 4 displays the observed $\beta$-conditioned means of (2.2) and the numerical solutions corresponding to the maximum $\mathcal {W}$. The numerical solutions and observations trend similarly with wavenumber, indicating the scale dependence of the effective collisionality has been well modelled. The parameters of the maximum (recorded in figure 4) do not correspond exactly to the weighted geometric means of $\mathcal {W}$ (seen in figure 3), reflecting the statistical nature of the measured quantities.

Figure 4. The panels (a–d) show the $\beta$-conditioned mean of the four quantities in (2.2) for the three median wavenumber bins $k_{\mathrm {SW}} = [0.288, 1.41, 6.34] \times 10^{-5} \ \mathrm {km}^{-1}$ as solid (black, blue, magenta) lines, respectively. Statistical uncertainties on the mean trends can be seen in figure 2. The dashed lines are the numerical solutions corresponding to the maximum $\mathcal {W}$; the parameters of the maximum are reported in the panels.

The method of calculating statistics for $\lambda _{\mathrm {mfp}}^{\mathrm {eff}}$, $\alpha$, $k_{\mathrm {iso}}$ displayed in figure 3 for $C_{\perp }$ produces similar statistics for $C_{\parallel }, A_{\parallel }, A_{\perp }$ (see Appendix C). Therefore, in table 1, combined statistics are reported. The measured effective mean-free-path and mean proton thermal speed (measured with this dataset) give an effective collision frequency of $\nu _{\mathrm {eff}} = v_{\mathrm {th}}^{\mathrm {p}} / \lambda _{\mathrm {mfp}}^{\mathrm {eff}}$ = 1.11 $\times 10^{-4}$ s$^{-1}$.

Table 1. Combined weighted geometric mean $\mu _x$, standard deviation $\sigma _{x,x}$ and the two sigma confidence interval $\mathrm {CI}_{x}$.

The transition frequency, where $\nu _{\mathrm {eff}} \simeq \omega$, can be estimated with $\nu _{\mathrm {eff}}$ and the ion-acoustic dispersion relation $\omega _{\mathrm {IA}} = k_{\parallel } \, c_{\mathrm {s}}$, giving the parallel transition wavenumber $k^{\mathrm {trans}}_{\parallel } = v_{\mathrm {th}}^{\mathrm {p}}/c_{\mathrm {s}} \, \lambda _{\mathrm {mfp}}^{\mathrm {eff}}$. Using the wavenumber model, (4.1), the transition wavenumber is

(4.4)\begin{equation} k^{\mathrm{trans}} = \frac{v_{\mathrm{th}}^{\mathrm{p}}}{c_{\mathrm{s}} \, \lambda_{\mathrm{mfp}}^{\mathrm{eff}} } \, \sqrt{1 + \left[\frac{2 \big( v_{\mathrm{th}}^{\mathrm{p}} \big)^{2} }{ \big(\lambda_{\mathrm{mfp}}^{\mathrm{eff}} \, k_{\mathrm{iso}} \, c_{\mathrm{s}}\big)^{2} } \right]^{(1 - \alpha)/\alpha} } \end{equation}

(more details are provided in Appendix D). Inserting the combined statistics from table 1, using a typical value of $v_{\mathrm {th}}^{\mathrm {p}} / c_{\mathrm {s}} = \sqrt {1/2}$ for the solar wind, and using the TFF assumption, the transition wavenumber in spacecraft-frame frequency at 1 AU is $\langle V_{\mathrm {SW}} \rangle \, k^{\mathrm {trans}} = f^{\mathrm {trans}} =0.19$ Hz and $\mathrm {CI}_{f^{\mathrm {trans}}} = [0.046, 0.33 ]$ Hz. The uncertainties are propagated from $V_{\mathrm {SW}}$ and the four estimates of $k^{\mathrm {trans}}$ from $C_{\parallel }, \, A_{\parallel }, \, C_{\perp }, \, A_{\perp }$.

5. Discussion

The relative non-conservation of the CGL invariants has been measured and the behaviour has been modelled with the slow-mode branch of the KMHD-BGK equations to measure the effective mean free path of the solar wind protons and the scale dependence of the slow-mode wavenumber anisotropy (table 1 reports the statistics of these measurements). The primary result of this Letter is the measured effective proton mean free path, which is ${\sim }10^{3}$ times smaller than the Spitzer–Härm mean free path ($\lambda _{\mathrm {mfp}}^{\mathrm {SH}} = 1.14 \times 10^{8} \ \mathrm {km}$, see Appendix A). Therefore, the fluid-like range in the solar wind extends to much smaller scales than the prediction based on particle collisions. In addition, the scale-dependent anisotropy of the compressive fluctuations ($\alpha \simeq 0.4$) is consistent with previous measurements (Chen et al. Reference Chen, Mallet, Schekochihin, Horbury, Wicks and Bale2012; Chen Reference Chen2016), being more anisotropic than the Alfvénic fluctuations, which follow the critical balance value $\alpha _{\mathrm {CB}} = 2/3$ (Goldreich & Sridhar Reference Goldreich and Sridhar1997).

The measured transition frequency, the scale between fluid behaviour ($f \ll f^{\mathrm {trans}}$) and collisionless behaviour ($f \gg f^{\mathrm {trans}}$), of $f^{\mathrm {trans}} = 0.19$ Hz is at the well-known break in power law $(k_{\perp } \rho _{\mathrm {p}} \sim 1)$ of the magnetic-field power spectrum at 1 AU (Leamon et al. Reference Leamon, Smith, Ness, Matthaeus and Wong1998; Kiyani et al. Reference Kiyani, Osman and Chapman2015; Verscharen et al. Reference Verscharen, Klein and Maruca2019). These measurements therefore justify the use of fluid MHD theory at larger scales $(k_{\perp } \rho _{\mathrm {p}} < 1)$ (Tu & Marsch Reference Tu and Marsch1995; Goldreich & Sridhar Reference Goldreich and Sridhar1997; Bruno & Carbone Reference Bruno and Carbone2013; Chen Reference Chen2016). If the result $k_{\perp } \rho _{\mathrm {p}} \simeq k_{\parallel } \lambda ^{\mathrm {eff}}_{\mathrm {mfp}}$ turns out to be a general property of weakly collisional plasma, this provides a simple parameterisation for the effective collisionality of astrophysical plasmas.

The method employed in this Letter relies on linear theory to describe cross-correlations and amplitude ratios of various plasma properties. While there is evidence that such linear quantities are approximately preserved in solar wind turbulence (e.g. Chen Reference Chen2016; Verscharen et al. Reference Verscharen, Chen and Wicks2017; Grošelj et al. Reference Grošelj, Chen, Mallet, Samtaney, Schneider and Jenko2019), and the numerical predictions in this Letter match the observations well, it would be interesting to study in the future the degree to which nonlinear effects may also contribute to these correlations. The BGK operator has been used in this work as a simple way to model effective collision processes, however, it is possible that the use of alternative collision operators may alter the numerical value of the effective mean free path obtained, although we would expect the order of magnitude result to hold. It should also be noted that the transition scale obtained here is consistent with previous observations of fluid-like behaviour in the solar wind above the ion gyroscale (Verscharen et al. Reference Verscharen, Chen and Wicks2017).

An important neglected effect is heating, which is needed to describe the solar wind temperature profile (Verma, Roberts & Goldstein Reference Verma, Roberts and Goldstein1995; Vasquez et al. Reference Vasquez, Smith, Hamilton, MacBride and Leamon2007). Heating would also break the CGL invariants through additional terms appearing on the right-hand side of (2.1) (Chandran et al. Reference Chandran, Dennis, Quataert and Bale2011; Hellinger et al. Reference Hellinger, Trávníček, Štverák, Matteini and Velli2013). The importance of this simplification can be addressed by comparing our measured effective collision time with the heating time inferred in previous papers (Vasquez et al. Reference Vasquez, Smith, Hamilton, MacBride and Leamon2007; Hellinger et al. Reference Hellinger, Trávníček, Štverák, Matteini and Velli2013). The heating time can be estimated from $Q_{\mathrm {heat}} / k_{\mathrm {B}} T_{\mathrm {p}} = \nu ^{\mathrm {heat}} \approx 10^{-6}\ {\rm s}^{-1}$, which is approximately $10^{2}$ times smaller than the effective collision frequency ($\nu _{\mathrm {eff}}$) measured in this Letter. This suggests isotropisation dominates over heating, which is not unreasonable given the extreme anisotropic evolution the CGL invariants would dictate due to expansion ($T_{\perp }^{\mathrm {p}} \propto R^{-2}, \; T_{\parallel }^{\mathrm {p}} \propto \mathrm {const.}$, where $R$ is the radial distance from the Sun; Matteini et al. Reference Matteini, Hellinger, Landi, Trávníček and Velli2012).

There are many possible mechanisms that could lead to the observed effective collision frequency. It is well known that large departures from the Maxwellian velocity distribution function invalidate the Spitzer–Härm approach (Marsch Reference Marsch2006), in particular, large gradients in velocity space lead to fast collisional thermalisation (Pezzi, Valentini & Veltri Reference Pezzi, Valentini and Veltri2016). However, given that the departure from Spitzer–Härm is a factor ${\approx }10^{3}$, and the fact that our analysis is based on the properties of the low-order moments of the velocity distribution function (which would not be strongly influenced by collisional effects; Pezzi et al. Reference Pezzi, Perrone, Servidio, Valentini, Sorriso-Valvo and Veltri2019), collisional processes are very unlikely to lead to the observed behaviour, implicating collisionless physics.

Previous works have suggested a range of possible effective collision processes that can arise in collisionless plasmas. These include wave–particle interactions (Kellogg Reference Kellogg2000; Graham et al. Reference Graham, Khotyaintsev, André, Vaivads, Divin, Drake, Norgren, Contel, Lindqvist and Rager2022), instabilities (Gary et al. Reference Gary, Yin and Winske2000; Yoon Reference Yoon2017) and the plasma wave echo (Schekochihin et al. Reference Schekochihin, Parker, Highcock, Dellar, Dorland and Hammett2016; Meyrand et al. Reference Meyrand, Kanekar, Dorland and Schekochihin2019). They have long been studied theoretically and numerically (Coroniti & Eviatar Reference Coroniti and Eviatar1977; Schekochihin & Cowley Reference Schekochihin and Cowley2006; Kunz, Schekochihin & Stone Reference Kunz, Schekochihin and Stone2014; Helander, Strumik & Schekochihin Reference Helander, Strumik and Schekochihin2016; Kunz, Stone & Quataert Reference Kunz, Stone and Quataert2016; Rincon et al. Reference Rincon, Califano, Schekochihin and Valentini2016; Squire, Quataert & Kunz Reference Squire, Quataert and Kunz2017), but it is an open question as to the relevant role of the various mechanisms and how they are activated (Verscharen et al. Reference Verscharen, Chandran, Klein and Quataert2016; Squire et al. Reference Squire, Kunz, Quataert and Schekochihin2017; Kunz et al. Reference Kunz, Squire, Schekochihin and Quataert2020). Therefore, further studies are necessary to assess exactly what key physics of a weakly collisional plasma leads to the measured effective collisionality, since most astrophysical plasmas, being multi-scale and turbulent, will support effective collision mechanisms (Zhuravleva et al. Reference Zhuravleva, Churazov, Schekochihin, Allen, Vikhlinin and Werner2019). The measurements presented here provide constraints to be satisfied by theories of effective collision processes.

Acknowledgements

We would like to thank S.D. Bale for pointing us to the dataset and L.B. Wilson III for helping us understand the dataset.

Editor Thierry Passot thanks the referees for their advice in evaluating this article.

Funding

J.T.C. was supported by a QMUL Principal Studentship. C.H.K.C. was supported by UKRI Future Leaders Fellowship MR/W007657/1, STFC Ernest Rutherford Fellowship ST/N003748/2, and STFC Consolidated Grant ST/T00018X/1. Support for J.S. was provided by Rutherford Discovery Fellowship RDF-U001804, which is managed through the Royal Society Te Apārangi.

Declaration of interests

The authors report no conflict of interest.

Appendix A. Collision length and time scales

Following the unit convention of Huba (Reference Huba1983), the Spitzer–Härm proton–proton collision frequency (Spitzer Reference Spitzer1962) for a proton–electron plasma with $T_{\mathrm {p}} \leqslant T_{\mathrm {e}}$, where $T_{\mathrm {p}} \, (T_{\mathrm {e}})$ is the proton (electron) temperature, is written

(A1)\begin{equation} \nu_{\mathrm{p},\mathrm{p}}^{\mathrm{SH}} = 4.8 \times 10^{{-}8} \, n_{\mathrm{p}} (k_{\mathrm{B}} T_{\mathrm{p}})^{{-}3/2} \, \lambda \, \big(\mathrm{s}^{{-}1}\big), \end{equation}

where $n_{\mathrm {p}} \ (\mathrm {cm}^{-3})$ is the proton number density, $k_{\mathrm {B}} \, T_{\mathrm {p}}$ is in eV and the Coulomb logarithm is $\lambda$. The Coulomb logarithm for proton–proton collisions

(A2)\begin{equation} \lambda = 23 - \ln \left| \frac{\sqrt{2 n_{\mathrm{p}}}}{T_{\mathrm{p}}^{3/2}} \right|. \end{equation}

The dataset described in § 3 provides the following averages:

(A3)\begin{gather} n_{\mathrm{p}} = 5.33 \, (\mathrm{cm}^{{-}3}), \end{gather}
(A4)\begin{gather}k_{\mathrm{B}} T_{\mathrm{p}} = 30.0 \, (\mathrm{eV}), \end{gather}
(A5)\begin{gather}v_{\mathrm{th}}^{\mathrm{p}} = 48.3 \, (\mathrm{km/s}), \end{gather}

where the proton thermal speed is $v_{\mathrm {th}}^{\mathrm {p}}$. With these measurements collision scales can be calculated

(A6)\begin{gather} \nu_{\mathrm{p},\mathrm{p}}^{\mathrm{SH}} = 4.23 \times 10^{{-}7} \, ({\rm s}^{{-}1}), \end{gather}
(A7)\begin{gather}\lambda_{\mathrm{mfp}}^{\mathrm{SH}} = v_{\mathrm{th}}^{\mathrm{p}} / \nu_{\mathrm{p},\mathrm{p}}^{\mathrm{SH}} = 1.14 \times 10^{8} \, (\mathrm{km}), \end{gather}

where $\lambda _{\mathrm {mfp}}^{\mathrm {SH}}$ is the Spitzer–Härm proton–proton mean free path.

Appendix B. Linear collisional-kinetic MHD

The kinetic magnetohydrodynamic (KMHD) equations are found in Kulsrud et al. (Reference Kulsrud, Sagdeev and Rosenbluth1980) where a BGK collision operator can be added (Snyder et al. Reference Snyder, Hammett and Dorland1997) to study wave modes of arbitrary collision frequency (Sharma et al. Reference Sharma, Hammett and Quataert2003). The BGK collision operator is defined as

(B1)\begin{equation} \mathcal{C}_{\mathrm{BGK}} \big[F_s(\boldsymbol{v}; n_s, T_s) , f_s(t, \boldsymbol{x}, \boldsymbol{v}) \big] = \nu^{s} \big[ F_s(\boldsymbol{v}; n_s, T_s) - f_s(t, \boldsymbol{x}, \boldsymbol{v}) \big], \end{equation}

where $F_s$ is the equilibrium distribution function, assumed to be a Maxwellian, parameterised by the density ($n_s$) and temperature ($T_s$) to conserve particle number and energy. The BGK collision operator approximates any process that restores the distribution function ($f_s$) to the equilibrium ($F_s$) at a rate of $\nu ^{s}$.

The so-called drift kinetic equation is derived by transforming into the bulk velocity frame and assuming the distribution function is gyrotropic so the background electric can be ignored (Kulsrud et al. Reference Kulsrud, Sagdeev and Rosenbluth1980). The equations are linearised on a static background and Fourier transformed to produce

(B2)\begin{gather} \omega \tilde{u}_{{\perp}} + \frac{1}{\beta} \big( {-} k_{{\perp}} \tilde{b}_{{\parallel}} + k_{{\parallel}} \tilde{b}_{{\perp}} \big) - \frac{ k_{{\perp}}}{2 \beta} \big( \tilde{p}_{{\perp}}^{p} + \tilde{p}_{{\perp}}^{e}) = 0, \end{gather}
(B3)\begin{gather}\omega \tilde{u}_{{\parallel}} - \frac{k_{{\parallel}} }{2 \beta} \tilde{p}_{{\parallel}} = 0, \end{gather}
(B4)\begin{gather}\omega \tilde{b}_{{\perp}} + k_{{\parallel}} \tilde{u}_{{\perp}} = 0, \end{gather}
(B5)\begin{gather}\omega \tilde{b}_{{\parallel}} - k_{{\perp}}\tilde{u}_{{\perp}} = 0, \end{gather}
(B6)\begin{gather}\omega \tilde{n} - \big( k_{{\parallel}} \tilde{u}_{{\parallel}} + k_{{\perp}} \tilde{u}_{{\perp}} \big) = 0, \end{gather}

where $\omega$ is the complex frequency, $\tilde {u}_{\perp } \ (\tilde {u}_{\parallel })$ is the perpendicular (parallel) bulk velocity, $k_{\perp } \ (k_{\parallel })$ is the perpendicular (parallel) wavenumber, $\beta$ is the proton beta, $\tilde {b}_{\perp } \ (\tilde {b}_{\parallel })$ is the perpendicular (parallel) magnetic field, $\tilde {p}^{ \mathrm {s}}_{\perp } (\tilde {p}^{\mathrm {s}}_{\parallel })$ is the perpendicular (parallel) species ‘s’ pressure and $\tilde {n}$ is the density (quasi-neutrality). The tilde denotes the Fourier amplitude. The equations are closed by taking density and pressure moments of the linear Fourier analysed drift kinetic equation, which produces

(B7)\begin{gather} \tilde{n} \big( 1 + \zeta^{s}_{\nu} \, \mathcal{Z}^{s} \big) - \frac{\tilde{p}^{s}_{{\perp}}}{\beta_s} \left(1 + \frac{2}{3} \zeta^{s}_{\nu} \, \mathcal{Z}^{s} \right) - \tilde{b}_{{\parallel}} \zeta^{s}_{\omega} \, \mathcal{Z}^{s} - \frac{\tilde{p}^{s}_{{\parallel}}}{\beta_s} \zeta^{s}_{\nu} \, \mathcal{Z}^{s} \frac{1}{3} = 0 \end{gather}
(B8)\begin{align} & \tilde{n} \left[1 + 2 (\zeta^{s})^{2} \mathcal{R}^{s} + \frac{3}{2}\zeta^{s}_{\nu} \big( \mathcal{Z}^{s} - 2 \zeta^{s} \mathcal{R}^{s} \big) \right] - \frac{\tilde{p}^{s}_{{\parallel}}}{\beta_s} \left[ \mathcal{R}^{s} + \frac{1}{6} \zeta^{s}_{\nu} \big( \mathcal{Z}^{s} - 2 \zeta^{s} \mathcal{R}^{s} \big) \right] \nonumber\\ & \quad - \tilde{b}_{{\parallel}} \left[ 1 + 2 (\zeta^{s})^{2} \mathcal{R}^{s} - \mathcal{R}^{s} + \zeta^{s}_{\nu} \big( \mathcal{Z}^{s} - 2 \zeta^{s} \mathcal{R}^{s} \big) \right] - \frac{\tilde{p}^{s}_{{\perp}}}{\beta_s} \frac{1}{3} \zeta^{s}_{\nu} \big( \mathcal{Z}^{s} - 2 \zeta^{s} \mathcal{R}^{s} \big) = 0, \end{align}

with the definitions

(B9)\begin{equation} \zeta^{s}_{\omega} = \frac{\omega }{ |k_{{\parallel}}| v_{\mathrm{th}}^{s}} , \quad \zeta^{s}_{\nu} = \frac{i\nu^{s}}{ |k_{{\parallel}}| v_{\mathrm{th}}^{s}} , \quad \zeta^{s} = \zeta^{s}_{\omega} + \zeta^{s}_{\nu} \end{equation}

and $\mathcal {R}^{s} = 1 + \zeta ^{s} \mathcal {Z}^{s}$. The plasma dispersion function is $\mathcal {Z}^{s}$ (Fried & Conte Reference Fried and Conte2015). Throughout the text $\beta$ is the proton beta and $\beta _{\mathrm {e}}$ is the electron beta. The kinetic equation for the electrons must be solved since the electron pressure appears in the momentum equation. The parameters relevant to the electrons are $T_{\mathrm {p}} / T_{\mathrm {e}}$ which is set to 1 and the effective mean free path species ratio $\lambda _{\mathrm {mfp}}^{\mathrm {eff}} / \lambda _{\mathrm {mfp,electrons}}$ which is set to 1, where the mean free path of the electrons is $\lambda _{\mathrm {mfp,electrons}}$. These equations form a linear system of equations that can be solved numerically and provide all the numerical solutions of the Letter.

Appendix C. Weighted geometric statistics

This appendix follows Norris (Reference Norris1940); Kendall & Stuart (Reference Kendall and Stuart1977). If the observations $x_i$ have unnormalised weights $w_i$, the definitions follow of the weighted geometric mean

(C1)\begin{equation} \mu^{x} = \exp \left\{ \sum_i^{n} \frac{ w_i \ln | x_i | }{ \sum_i^{n} w_i} \right\}, \end{equation}

weighted geometric covariance matrix

(C2)\begin{equation} \big(\sigma^{x,y} \big)^{2} = \exp \left\{ \frac{1}{\sum_i^{n} w_i } \sum_i^{n} w_i \ln \left| \frac{x_i}{\mu^{x}} \right| \ln \left| \frac{y_i}{\mu^{y}} \right| \right\}, \end{equation}

and the two sigma standard deviation

(C3)\begin{equation} \ln |\mu^{x} | \pm 2 \ln |(\sigma^{x,x})| \ \Rightarrow \ \mathrm{CI}^{x} = [ \mu^{x} \, (\sigma^{x,x})^{2} , \, \mu^{x} /( \sigma^{x,x})^{2} ], \end{equation}

where $\mathrm {CI}^{x}$ is the weighted geometric confidence interval. The statistics detailed here are used to calculate the main results of the Letter, which are reported in table 1.

Figure 5 shows that the statistics of $\alpha, k_{\mathrm {iso}}, \lambda _{\mathrm {mfp}}^{\mathrm {eff}}$ for $C_{\perp }, C_{\parallel }, A_{\perp }, A_{\parallel }$ are similar so that combined statistics are reported in table 1. Figure 5(b,d,f) shows the normalised weighted geometric covariance between the model parameters

(C4)\begin{equation} \big( \hat{\sigma}^{x,y} \big)^{2} = \frac{\big( \sigma^{x,y} \big)^{2}}{ \sigma^{x,x} \, \sigma^{y,y}}. \end{equation}

These terms are small.

Figure 5. The weighted geometric means, (C1), are plotted in (a,c,e) as circles and the confidence intervals, (C3), are plotted as a vertical lines. Panels (b,d,f) are the non-diagonal terms of the normalised weighted covariance matrix, (C4).

Appendix D. Wavenumber model

The model introduced here $k_{\parallel } \sim k_{\perp }^{\alpha }$ is generalised from the critical balance model of Alfvénic turbulence (Goldreich & Sridhar Reference Goldreich and Sridhar1995). In this Letter it is used to model the compressive wave propagation angle $\theta _{\hat {{\boldsymbol {b}}}, \hat {{\boldsymbol {k}}}}$. To ensure the isotropic wavenumber ($k_{\mathrm {iso}} = k$ when $k_{\perp } = k_{\parallel }$) is defined correctly

(D1)\begin{equation} \frac{k_{{\parallel}}}{k_{\mathrm{iso}} / \sqrt{2} } = \left(\frac{k_{{\perp}}}{k_{\mathrm{iso}} / \sqrt{2}} \right)^{\alpha}, \end{equation}

which leads to

(D2)\begin{equation} k = \frac{k_{\mathrm{iso}}}{ \sqrt{2}} \cos(\theta_{\hat{{\boldsymbol{b}}}, \hat{{\boldsymbol{k}}}})^{1 / (\alpha-1)} \sin(\theta_{\hat{{\boldsymbol{b}}}, \hat{{\boldsymbol{k}}}})^{\alpha / (1-\alpha)}, \end{equation}

which appears as (4.1). Here, $k$ depends on $\theta _{\hat {{\boldsymbol {b}}}, \hat {{\boldsymbol {k}}}}$ parametrised by $\alpha \in [0,1), \ k_{\mathrm {iso}}$. Equation (D2) can be inverted on $\theta _{\hat {{\boldsymbol {b}}}, \hat {{\boldsymbol {k}}}} \in [0,90^{\circ })$ for $k$.

The wavenumber model is also used in the derivation of (4.4) of the Letter. Just above (4.4) the relation

(D3)\begin{equation} k^{\mathrm{trans}}_{{\parallel}} \lambda_{\mathrm{mfp}}^{\mathrm{eff}} = v_{\mathrm{th}}^{\mathrm{p}} / c_{\mathrm{s}}, \end{equation}

is argued to define $k_{\parallel }^{\mathrm {trans}}$, which can be compared with measurements with the full wavenumber $k^{\mathrm {trans}}$. Using the model, (D2), to write

(D4)\begin{equation} \frac{v_{\mathrm{th}}^{\mathrm{p}} }{ c_{\mathrm{s}} \, \lambda_{\mathrm{mfp}}^{\mathrm{eff}} } = k^{\mathrm{trans}} \cos (\theta_{\hat{{\boldsymbol{b}}}, \hat{{\boldsymbol{k}}}}^{\mathrm{trans}}) = \frac{k_{\mathrm{iso}}}{ \sqrt{2}} \tan(\theta_{\hat{{\boldsymbol{b}}}, \hat{{\boldsymbol{k}}}}^{\mathrm{trans}})^{\alpha / (1-\alpha)}, \end{equation}

solving for $\theta _{\hat {{\boldsymbol {b}}}, \hat {{\boldsymbol {k}}}}^{\mathrm {trans}}$

(D5)\begin{equation} \theta_{\hat{{\boldsymbol{b}}}, \hat{{\boldsymbol{k}}}}^{\mathrm{trans}} = \mathrm{arctan} \left\{ \left[\frac{ \sqrt{2} v_{\mathrm{th}}^{\mathrm{p}} }{ c_{\mathrm{s}} \, k_{\mathrm{iso}} \, \lambda_{\mathrm{mfp}}^{\mathrm{eff}} } \right]^{(1-\alpha)/\alpha} \right \}, \end{equation}

then $k^{\mathrm {trans}}$ can be written

(D6)\begin{equation} k^{\mathrm{trans}} = \frac{k_{\mathrm{iso}}}{ \sqrt{2}} \cos(\theta_{\hat{{\boldsymbol{b}}}, \hat{{\boldsymbol{k}}}}^{\mathrm{trans}})^{1 / \alpha-1} \sin(\theta_{\hat{{\boldsymbol{b}}}, \hat{{\boldsymbol{k}}}}^{\mathrm{trans}})^{\alpha / 1-\alpha}. \end{equation}

Using trigonometric identities the transition wavenumber is,

(D7)\begin{equation} k^{\mathrm{trans}} = \frac{ v_{\mathrm{th}}^{\mathrm{p}} }{ c_{\mathrm{s}} \, \lambda_{\mathrm{mfp}}^{\mathrm{eff}} } \, \sqrt{1 + \left[\frac{ 2 ( v_{\mathrm{th}}^{\mathrm{p}})^{2} }{ c_{\mathrm{s}}^{2} \, k_{\mathrm{iso}}^{2} \, (\lambda_{\mathrm{mfp}}^{\mathrm{eff}})^{2} } \right]^{(1 - \alpha)/\alpha} }. \end{equation}

This appears as (4.4) of the letter.

References

REFERENCES

Bale, S.D., Kasper, J.C., Howes, G.G., Quataert, E., Salem, C. & Sundkvist, D. 2009 Magnetic fluctuation power near proton temperature anisotropy instability thresholds in the solar wind. Phys. Rev. Lett. 103 (21), 211101.CrossRefGoogle ScholarPubMed
Barnes, A. 1966 Collisionless damping of hydromagnetic waves. Phys. Fluids 9 (8), 1483–1495.CrossRefGoogle Scholar
Bhatnagar, P.L., Gross, E.P. & Krook, M. 1954 A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94 (3), 511–525.CrossRefGoogle Scholar
Bruno, R. & Carbone, V. 2013 The solar wind as a turbulence laboratory. Living Rev. Sol. Phys. 10 (1), 2.CrossRefGoogle Scholar
Chandran, B.D.G., Dennis, T.J., Quataert, E. & Bale, S.D. 2011 Incorporating kinetic physics into a two-fluid solar-wind model with temperature anisotropy and low-frequency Alfven-wave turbulence. Astrophys. J. 743 (2), 197.CrossRefGoogle Scholar
Chen, C.H.K. 2016 Recent progress in astrophysical plasma turbulence from solar wind observations. J. Plasma Phys. 82 (6), 535820602.CrossRefGoogle Scholar
Chen, C.H.K., Mallet, A., Schekochihin, A.A., Horbury, T.S., Wicks, R.T. & Bale, S.D. 2012 Three-dimensional structure of solar wind turbulence. Astrophys. J. 758 (2), 120.CrossRefGoogle Scholar
Chen, C.H.K., Matteini, L., Schekochihin, A.A., Stevens, M.L., Salem, C.S., Maruca, B.A., Kunz, M.W. & Bale, S.D. 2016 Multi-species measurements of the firehose and mirror instability thresholds in the solar wind. Astrophys. J. Lett. 825 (2), L26.CrossRefGoogle Scholar
Chew, G.F., Goldberger, M.L. & Low, F.E. 1956 The Boltzmann equation and the one-fluid hydromagnetic equations in the absence of particle collisions. Proc. R. Soc. Lond. A 236 (1204), 112–118.Google Scholar
Coburn, J.T., Smith, C.W., Vasquez, B.J., Stawarz, J.E. & Forman, M.A. 2012 The turbulent cascade and proton heating in the solar wind during solar minimum. Astrophys. J. 754 (2), 93.CrossRefGoogle Scholar
Coleman, P.J. Jr., 1968 Turbulence, viscosity, and dissipation in the solar-wind plasma. Astrophys. J. 153, 371.CrossRefGoogle Scholar
Coroniti, F.V. & Eviatar, A. 1977 Magnetic field reconnection in a collisionless plasma. Astrophys. J. Suppl. 33, 189–210.CrossRefGoogle Scholar
Fried, B.D. & Conte, S.D. 2015 The Plasma Dispersion Function: The Hilbert Transform of the Gaussian. Academic.Google Scholar
Gary, S.P., Yin, L. & Winske, D. 2000 Electromagnetic proton cyclotron anisotropy instability: wave-particle scattering rate. Geophys. Res. Lett. 27 (16), 2457–2459.CrossRefGoogle Scholar
Goldreich, P. & Sridhar, S. 1995 Toward a theory of interstellar turbulence. II. Strong Alfvenic turbulence. Astrophys. J. 438, 763.CrossRefGoogle Scholar
Goldreich, P. & Sridhar, S. 1997 Magnetohydrodynamic turbulence revisited. Astrophys. J. 485 (2), 680–688.CrossRefGoogle Scholar
Graham, D.B., Khotyaintsev, Y.V., André, M., Vaivads, A., Divin, A., Drake, J.F., Norgren, C., Contel, O.L., Lindqvist, P.-A., Rager, A.C., et al. 2022 Direct observations of anomalous resistivity and diffusion in collisionless plasma. Nat. Commun. 13 (1), 2954.CrossRefGoogle ScholarPubMed
Griffel, D.H. & Davis, L. 1969 The anisotrophy of the solar wind. Planet. Space Sci. 17 (5), 1009–1020.CrossRefGoogle Scholar
Grošelj, D., Chen, C.H., Mallet, A., Samtaney, R., Schneider, K. & Jenko, F. 2019 Kinetic turbulence in astrophysical plasmas: waves and/or structures? Phys. Rev. X 9 (3), 031037.Google Scholar
Gross, E.P. & Krook, M. 1956 Model for collision processes in gases: small-amplitude oscillations of charged two-component systems. Phys. Rev. 102 (3), 593–604.CrossRefGoogle Scholar
Hamasaki, S. & Krall, N.A. 1973 Relaxation of anisotropic collisionless plasma. Phys. Fluids 16 (1), 145–149.CrossRefGoogle Scholar
Helander, P., Strumik, M. & Schekochihin, A.A. 2016 Constraints on dynamo action in plasmas. J. Plasma Phys. 82 (6), 905820601.CrossRefGoogle Scholar
Hellinger, P., Trávníček, P., Kasper, J.C. & Lazarus, A.J. 2006 Solar wind proton temperature anisotropy: linear theory and WIND/SWE observations. Geophys. Res. Lett. 33 (9), L09101.CrossRefGoogle Scholar
Hellinger, P., Trávníček, P.M., Štverák, V., Matteini, L. & Velli, M. 2013 Proton thermal energetics in the solar wind: helios reloaded. J. Geophys. Res. 118 (4), 1351–1365.CrossRefGoogle Scholar
Howes, G.G., Bale, S.D., Klein, K.G., Chen, C.H.K., Salem, C.S. & TenBarge, J.M. 2012 The slow-mode nature of compressible wave power in solar wind turbulence. Astrophys. J. Lett. 753 (1), L19.CrossRefGoogle Scholar
Howes, G.G., Cowley, S.C., Dorland, W., Hammett, G.W., Quataert, E. & Schekochihin, A.A. 2006 Astrophysical gyrokinetics: basic equations and linear theory. Astrophys. J. 651 (1), 590–614.CrossRefGoogle Scholar
Huba, J. D. 1983 NRL (Naval Research Laboratory) plasma formulary, revised. Tech. Rep. Naval Research Lab, Washington DC.Google Scholar
Hunana, P., Tenerani, A., Zank, G.P., Khomenko, E., Goldstein, M.L., Webb, G.M., Cally, P.S., Collados, M., Velli, M. & Adhikari, L. 2019 An introductory guide to fluid models with anisotropic temperatures. Part 1. CGL description and collisionless fluid hierarchy. J. Plasma Phys. 85 (6), 205850602.CrossRefGoogle Scholar
Kasper, J.C., Lazarus, A.J. & Gary, S.P. 2002 Wind/SWE observations of firehose constraint on solar wind proton temperature anisotropy. Geophys. Res. Lett. 29 (17), 1839.CrossRefGoogle Scholar
Kellogg, P.J. 2000 Fluctuations and ion isotropy in the solar wind. Astrophys. J. 528 (1), 480–485.CrossRefGoogle Scholar
Kellogg, P.J. & Horbury, T.S. 2005 Rapid density fluctuations in the solar wind. Ann. Geophys. 23 (12), 3765.CrossRefGoogle Scholar
Kendall, M.G. & Stuart, A. 1977 The Advanced Theory of Statistics. Vol. 1: Distribution Theory. Macmillan.Google Scholar
Kiyani, K.H., Osman, K.T. & Chapman, S.C. 2015 Dissipation and heating in solar wind turbulence: from the macro to the micro and back again. Phil. Trans. R. Soc. Lond. A 373 (2041), 20140155.Google Scholar
Klein, K.G., Howes, G.G., TenBarge, J.M., Bale, S.D., Chen, C.H.K. & Salem, C.S. 2012 Using synthetic spacecraft data to interpret compressible fluctuations in solar wind turbulence. Astrophys. J. 755 (2), 159.CrossRefGoogle Scholar
Kulsrud, R.M., Sagdeev, R.N. & Rosenbluth, M.N. 1980 MHD Description of Plasma: Handbook of Plasma Physics. North–Holland.CrossRefGoogle Scholar
Kunz, M.W., Schekochihin, A.A. & Stone, J.M. 2014 Firehose and mirror instabilities in a collisionless shearing plasma. Phys. Rev. Lett. 112 (20), 205003.CrossRefGoogle Scholar
Kunz, M.W., Squire, J., Schekochihin, A.A. & Quataert, E. 2020 Self-sustaining sound in collisionless, high-${\beta }$ plasma. J. Plasma Phys. 86 (6), 905860603.CrossRefGoogle Scholar
Kunz, M.W., Stone, J.M. & Quataert, E. 2016 Magnetorotational turbulence and dynamo in a collisionless plasma. Phys. Rev. Lett. 117 (23), 235101.CrossRefGoogle Scholar
Leamon, R.J., Smith, C.W., Ness, N.F., Matthaeus, W.H. & Wong, H.K. 1998 Observational constraints on the dynamics of the interplanetary magnetic field dissipation range. J. Geophys. Res. 103 (A3), 4775–4787.CrossRefGoogle Scholar
Lepping, R., Acũna, M., Burlaga, L., Farrell, W., Slavin, J., Schatten, K., Mariani, F., Ness, N., Neubauer, F., Whang, Y., et al. 1995 The wind magnetic field investigation. Space Sci. Rev. 71 (1-4), 207–229.CrossRefGoogle Scholar
Lin, R.P., Anderson, K.A., Ashford, S., Carlson, C., Curtis, D., Ergun, R., Larson, D., McFadden, J., McCarthy, M., Parks, G.K., et al. 1995 A three-dimensional plasma and energetic particle investigation for the wind spacecraft. Space Sci. Rev. 71 (1–4), 125–153.CrossRefGoogle Scholar
Lithwick, Y. & Goldreich, P. 2001 Compressible magnetohydrodynamic turbulence in interstellar plasmas. Astrophys. J. 562 (1), 279–296.CrossRefGoogle Scholar
MacBride, B.T., Smith, C.W. & Forman, M.A. 2008 The turbulent cascade at 1 AU: energy transfer and the third-order scaling for MHD. Astrophys. J. 679 (2), 1644–1660.CrossRefGoogle Scholar
Marsch, E. 2006 Kinetic physics of the solar corona and solar wind. Living Rev. Sol. Phys. 3 (1), 1.CrossRefGoogle Scholar
Marsch, E., Muehlhaeuser, K.H., Rosenbauer, H. & Schwenn, R. 1983 On the equation of state of solar wind ions derived from helios measurements. J. Geophys Res. 88 (A4), 2982–2992.CrossRefGoogle Scholar
Marsch, E. & Tu, C.Y. 1990 Spectral and spatial evolution of compressible turbulence in the inner solar wind. J. Geophys. Res. 95 (A8), 11945–11956.CrossRefGoogle Scholar
Matteini, L., Hellinger, P., Landi, S., Trávníček, P.M. & Velli, M. 2012 Ion kinetics in the solar wind: coupling global expansion to local microphysics. Space Sci. Rev. 172 (1–4), 373–396.CrossRefGoogle Scholar
Matthaeus, W.H., Dasso, S., Weygand, J.M., Kivelson, M.G. & Osman, K.T. 2010 Eulerian decorrelation of fluctuations in the interplanetary magnetic field. Astrophys. J. Lett. 721 (1), L10–L13.CrossRefGoogle Scholar
Matthaeus, W.H. & Goldstein, M.L. 1982 Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind. J. Geophys. Res. 87 (A8), 6011–6028.CrossRefGoogle Scholar
Matthaeus, W.H., Zank, G.P., Smith, C.W. & Oughton, S. 1999 Turbulence, spatial transport, and heating of the solar wind. Phys. Rev. Lett. 82 (17), 3444–3447.CrossRefGoogle Scholar
Meyrand, R., Kanekar, A., Dorland, W. & Schekochihin, A.A. 2019 Fluidization of collisionless plasma turbulence. Proc. Natl Acad. Sci. USA 116 (4), 1185–1194.CrossRefGoogle ScholarPubMed
Montgomery, D., Brown, M.R. & Matthaeus, W.H. 1987 Density fluctuation spectra in magnetohydrodynamic turbulence. J. Geophys. Res. 92 (A1), 282–284.CrossRefGoogle Scholar
Nicolaou, G., Livadiotis, G., Wicks, R.T., Verscharen, D. & Maruca, B.A. 2020 Polytropic behavior of solar wind protons observed by Parker solar probe. Astrophys. J. 901 (1), 26.CrossRefGoogle Scholar
Nishida, A. 1969 Thermal state and effective collision frequency in the solar wind plasma. J. Geophys. Res. 74 (21), 5155.CrossRefGoogle Scholar
Norris, N. 1940 The standard errors of the geometric and harmonic means and their application to index numbers. Ann. Stat. 11 (4), 445–448.CrossRefGoogle Scholar
Parker, E.N. 1958 Dynamics of the interplanetary gas and magnetic fields. Astrophys. J. 128, 664.CrossRefGoogle Scholar
Pezzi, O., Perrone, D., Servidio, S., Valentini, F., Sorriso-Valvo, L. & Veltri, P. 2019 Proton–proton collisions in the turbulent solar wind: hybrid Boltzmann–Maxwell simulations. Astrophys. J. 887 (2), 208.CrossRefGoogle Scholar
Pezzi, O., Valentini, F. & Veltri, P. 2016 Collisional relaxation of fine velocity structures in plasmas. Phys. Rev. Lett. 116 (14), 145001.CrossRefGoogle ScholarPubMed
Quataert, E. 2003 Radiatively inefficient accretion flow models of Sgr A*. Astron. Nachr. 324 (1), 435–443.CrossRefGoogle Scholar
Rincon, F., Califano, F., Schekochihin, A.A. & Valentini, F. 2016 Turbulent dynamo in a collisionless plasma. Proc. Natl Acad. Sci. USA 113 (15), 3950–3953.CrossRefGoogle Scholar
Schekochihin, A.A. & Cowley, S.C. 2006 Turbulence, magnetic fields, and plasma physics in clusters of galaxies. Phys. Plasmas 13 (5), 056501.CrossRefGoogle Scholar
Schekochihin, A.A., Cowley, S.C., Dorland, W., Hammett, G.W., Howes, G.G., Quataert, E. & Tatsuno, T. 2009 Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. 182 (1), 310–377.CrossRefGoogle Scholar
Schekochihin, A.A., Cowley, S.C., Kulsrud, R.M., Hammett, G.W. & Sharma, P. 2005 Plasma instabilities and magnetic field growth in clusters of galaxies. Astrophys. J. 629 (1), 139–142.CrossRefGoogle Scholar
Schekochihin, A.A., Parker, J.T., Highcock, E.G., Dellar, P.J., Dorland, W. & Hammett, G.W. 2016 Phase mixing versus nonlinear advection in drift-kinetic plasma turbulence. J. Plasma Phys. 82 (2), 905820212.CrossRefGoogle Scholar
Sharma, P., Hammett, G.W. & Quataert, E. 2003 Transition from collisionless to collisional magnetorotational instability. Astrophys. J. 596 (2), 1121–1130.CrossRefGoogle Scholar
Snyder, P.B., Hammett, G.W. & Dorland, W. 1997 Landau fluid models of collisionless magnetohydrodynamics. Phys. Plasmas 4 (11), 3974–3985.CrossRefGoogle Scholar
Spitzer, L. 1962 Physics of Fully Ionized Gases. Courier Corporation.Google Scholar
Squire, J., Kunz, M.W., Quataert, E. & Schekochihin, A.A. 2017 Kinetic simulations of the interruption of large-amplitude shear-Alfvén waves in a high-${\beta }$ plasma. Phys. Rev. Lett. 119 (15), 155101.CrossRefGoogle Scholar
Squire, J., Quataert, E. & Kunz, M.W. 2017 Pressure-anisotropy-induced nonlinearities in the kinetic magnetorotational instability. J. Plasma Phys. 83 (6), 905830613.CrossRefGoogle ScholarPubMed
Stawarz, J.E., Smith, C.W., Vasquez, B.J., Forman, M.A. & MacBride, B.T. 2009 The turbulent cascade and proton heating in the solar wind at 1 AU. Astrophys. J. 697 (2), 1119–1127.CrossRefGoogle Scholar
Taylor, G.I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164 (919), 476–490.CrossRefGoogle Scholar
Totten, T.L., Freeman, J.W. & Arya, S. 1995 An empirical determination of the polytropic index for the free-streaming solar wind using Helios 1 data. J. Geophys. Res. 100 (A1), 13–18.CrossRefGoogle Scholar
Tu, C.-Y. & Marsch, E. 1995 Mhd structures, waves and turbulence in the solar wind: observations and theories. Space Sci. Rev. 73 (1–2), 1–210.CrossRefGoogle Scholar
Tu, C.Y. & Marsch, E. 2002 Anisotropy regulation and plateau formation through pitch angle diffusion of solar wind protons in resonance with cyclotron waves. J. Geophys Res. 107 (A9), 1249.CrossRefGoogle Scholar
Vasquez, B.J., Smith, C.W., Hamilton, K., MacBride, B.T. & Leamon, R.J. 2007 Evaluation of the turbulent energy cascade rates from the upper inertial range in the solar wind at 1 AU. J. Geophys. Res. 112 (A7), A07101.CrossRefGoogle Scholar
Verma, M.K., Roberts, D.A. & Goldstein, M.L. 1995 Turbulent heating and temperature evolution in the solar wind plasma. J. Geophys. Res. 100 (A10), 19839–19850.CrossRefGoogle Scholar
Verscharen, D., Chandran, B.D.G., Klein, K.G. & Quataert, E. 2016 Collisionless isotropization of the solar-wind protons by compressive fluctuations and plasma instabilities. Astrophys. J. 831 (2), 128.CrossRefGoogle Scholar
Verscharen, D., Chen, C.H.K. & Wicks, R.T. 2017 On kinetic slow modes, fluid slow modes, and pressure-balanced structures in the solar wind. Astrophys. J. 840 (2), 106.CrossRefGoogle Scholar
Verscharen, D., Klein, K.G. & Maruca, B.A. 2019 The multi-scale nature of the solar wind. Living Rev. Sol. Phys. 16 (1), 5.CrossRefGoogle ScholarPubMed
Yao, S., He, J.S., Marsch, E., Tu, C.Y., Pedersen, A., Rème, H. & Trotignon, J.G. 2011 Multi-scale anti-correlation between electron density and magnetic field strength in the solar wind. Astrophys. J. 728 (2), 146.CrossRefGoogle Scholar
Yao, S., He, J.S., Tu, C.Y., Wang, L.H. & Marsch, E. 2013 a Small-scale pressure-balanced structures driven by mirror-mode waves in the solar wind. Astrophys. J. 776 (2), 94.CrossRefGoogle Scholar
Yao, S., He, J.S., Tu, C.Y., Wang, L.H. & Marsch, E. 2013 b Small-scale pressure-balanced structures driven by oblique slow mode waves measured in the solar wind. Astrophys. J. 774 (1), 59.CrossRefGoogle Scholar
Yoon, P.H. 2017 Kinetic instabilities in the solar wind driven by temperature anisotropies. Rev. Mod. Plasma Phys. 1 (1), 4.CrossRefGoogle Scholar
Zank, G.P., Matthaeus, W.H. & Smith, C.W. 1996 Evolution of turbulent magnetic fluctuation power with heliospheric distance. J. Geophys. Res. 101 (A8), 17093–17108.CrossRefGoogle Scholar
Zhuravleva, I., Churazov, E., Schekochihin, A.A., Allen, S.W., Vikhlinin, A. & Werner, N. 2019 Suppressed effective viscosity in the bulk intergalactic plasma. Nat. Astron. 3, 832–837.CrossRefGoogle Scholar
Figure 0

Figure 1. Numerical solutions of the KMHD-BGK equations for a range of $k_{\parallel } \lambda _{\mathrm {mfp}}^{\mathrm {eff}}$ (see colour bar). The imaginary (real) part of the complex frequency is denoted $\gamma \ (\omega _r)$. The dotted (dashed) magenta lines are the long (short) limit of $\lambda _{\mathrm {mfp}}^{\mathrm {eff}}$ corresponding to the collisionless (collisional) slow-mode/ion-acoustic branch for $\theta _{\hat {\boldsymbol {b}},\hat {\boldsymbol {k}}} = 88^{\circ }$ (Howes et al.2006; Verscharen et al.2017).

Figure 1

Figure 2. The $\beta$-conditioned probability functions of the quantities in (2.2) for the wavenumber bin $k_{\mathrm {SW}} = 0.288 \times 10^{-5} \ \mathrm {km}^{-1}$. The thin black line is a contour of probability equal to 0.01. The magenta lines are mean (dashed), median (solid) and maximum (dotted) conditioned on $\beta$.

Figure 2

Figure 3. The three panels display the integrated weight volume, (4.3), for each parameter $\chi$, for $C_{\perp }$. The magenta crosses indicate the weighted geometric means and two sigma confidence intervals.

Figure 3

Figure 4. The panels (a–d) show the $\beta$-conditioned mean of the four quantities in (2.2) for the three median wavenumber bins $k_{\mathrm {SW}} = [0.288, 1.41, 6.34] \times 10^{-5} \ \mathrm {km}^{-1}$ as solid (black, blue, magenta) lines, respectively. Statistical uncertainties on the mean trends can be seen in figure 2. The dashed lines are the numerical solutions corresponding to the maximum $\mathcal {W}$; the parameters of the maximum are reported in the panels.

Figure 4

Table 1. Combined weighted geometric mean $\mu _x$, standard deviation $\sigma _{x,x}$ and the two sigma confidence interval $\mathrm {CI}_{x}$.

Figure 5

Figure 5. The weighted geometric means, (C1), are plotted in (a,c,e) as circles and the confidence intervals, (C3), are plotted as a vertical lines. Panels (b,d,f) are the non-diagonal terms of the normalised weighted covariance matrix, (C4).