Hostname: page-component-f554764f5-nwwvg Total loading time: 0 Render date: 2025-04-20T04:40:26.317Z Has data issue: false hasContentIssue false
  • English
  • Français

Pushforward of structure sheaf and virtual global generation

Part of: Curves

Published online by Cambridge University Press:  18 April 2024

Indranil Biswas ,
Manish Kumar  and
A. J. Parameswaran
Indranil Biswas*
Affiliation:
Department of Mathematics, Shiv Nadar University, Greater Noida, Uttar Pradesh, India
Manish Kumar
Affiliation:
Statistics and Mathematics Unit, Indian Statistical Institute, Bangalore, India
A. J. Parameswaran
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Bombay, India
*
Corresponding author: Indranil Biswas, email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 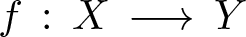$f\,:\,X\,\longrightarrow \,Y$ be a generically smooth morphism between irreducible smooth projective curves over an algebraically closed field of arbitrary characteristic. We prove that the vector bundle 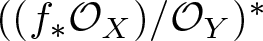$((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is virtually globally generated. Moreover, 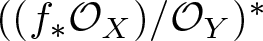$((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is ample if and only if f is genuinely ramified.

Keywords

virtual global generationgenuinely ramified mapampleness

MSC classification

Primary: 14H30: Coverings, fundamental group 14H60: Vector bundles on curves and their moduli
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 3 , August 2024 , pp. 663 - 673
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Biswas, I., A criterion for ample vector bundles over a curve in positive characteristic, Bull. Sci. Math. 129 (2005), 539–543.CrossRefGoogle Scholar
Biswas, I. and Parameswaran, A. J., On the ample vector bundles over curves in positive characteristic, C. R. Math. Acad. Sci. Paris 339 (2004), 355–358.CrossRefGoogle Scholar
Biswas, I. and Parameswaran, A. J., A criterion for virtual global generation, Ann. Sc. Norm. Super. Pisa Cl. Sci. 5 (2006), 39–53.Google Scholar
Biswas, I. and Parameswaran, A. J., Ramified covering maps and stability of pulled back bundles, Int. Math. Res. Not. 2022(17) (2022), 12821–12851.CrossRefGoogle Scholar
Coskun, I., Larson, E. and Vogt, I., Stability of Tschirnhausen bundles, arXiv:2207.07257.Google Scholar
Hartshorne, R., Ample vector bundles on curves, ample vector bundles, Publ. Math. Inst. Hautes Études Sci. 29 (1966), 63–94.CrossRefGoogle Scholar
Hartshorne, R., Ample vector bundles on curves, Nagoya Math. J. 43 (1971), 73–89.CrossRefGoogle Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, Vol. 52 (Springer-Verlag, New York-Heidelberg, 1977).CrossRefGoogle Scholar
Huybrechts, D. and Lehn, M., The Geometry of Moduli Spaces of Sheaves, Aspects of Mathematics, E31 (Friedr. Vieweg & Sons, Braunschweig, 1997).CrossRefGoogle Scholar
Narasimhan, M. S. and Seshadri, C. S., Stable and unitary vector bundles on a compact Riemann surface, Ann. Math. 82 (1965), 540–567.CrossRefGoogle Scholar
Serre, J.-P., Géométrie algébrique et géométrie analytique, Ann. Inst. Fourier 6 (1956), 1–42.CrossRefGoogle Scholar