Regrettably there are several errors in our paper. We present the corrections for the Appendix first as they are the source of some of the errors in the main body of the paper.
Appendix A. Endless integrals
The second term in the  $\unicode[STIX]{x1D705}\rightarrow 1$ limit of
$\unicode[STIX]{x1D705}\rightarrow 1$ limit of  $\overline{\cos \unicode[STIX]{x1D703}}$ in (A 50) should be to the minus one power with a prefactor of
$\overline{\cos \unicode[STIX]{x1D703}}$ in (A 50) should be to the minus one power with a prefactor of  $1/4$ rather than
$1/4$ rather than  $1/2$.
$1/2$.
The sign should be positive in the last form of (A 53) and both forms of (A 54).
Following (A 59), add the remark that ‘The  $\unicode[STIX]{x1D717}$-independent contribution of order
$\unicode[STIX]{x1D717}$-independent contribution of order  $\unicode[STIX]{x1D700}$ is neglected’.
$\unicode[STIX]{x1D700}$ is neglected’.
Equation (A 61) should be
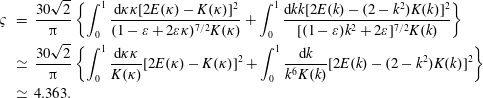 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70D} & = & \displaystyle \frac{30\sqrt{2}}{\unicode[STIX]{x03C0}}\left\{\int _{0}^{1}\frac{\text{d}\unicode[STIX]{x1D705}\unicode[STIX]{x1D705}[2\mathit{E}(\unicode[STIX]{x1D705})-\mathit{K}(\unicode[STIX]{x1D705})]^{2}}{(1-\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D700}\unicode[STIX]{x1D705})^{7/2}\mathit{K}(\unicode[STIX]{x1D705})}+\int _{0}^{1}\frac{\text{d}\mathit{kk}[2\mathit{E}(\mathit{k})-(2-\mathit{k}^{2})\mathit{K}(\mathit{k})]^{2}}{[(1-\unicode[STIX]{x1D700})\mathit{k}^{2}+2\unicode[STIX]{x1D700}]^{7/2}\mathit{K}(\mathit{k})}\right\}\nonumber\\ \displaystyle & \simeq & \displaystyle \frac{30\sqrt{2}}{\unicode[STIX]{x03C0}}\left\{\int _{0}^{1}\frac{\text{d}\unicode[STIX]{x1D705}\unicode[STIX]{x1D705}}{\mathit{K}(\unicode[STIX]{x1D705})}[2\mathit{E}(\unicode[STIX]{x1D705})-\mathit{K}(\unicode[STIX]{x1D705})]^{2}+\int _{0}^{1}\frac{\text{d}\mathit{k}}{\mathit{k}^{6}\mathit{K}(\mathit{k})}[2\mathit{E}(\mathit{k})-(2-\mathit{k}^{2})\mathit{K}(\mathit{k})]^{2}\right\}\nonumber\\ \displaystyle & \simeq & \displaystyle 4.363.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70D} & = & \displaystyle \frac{30\sqrt{2}}{\unicode[STIX]{x03C0}}\left\{\int _{0}^{1}\frac{\text{d}\unicode[STIX]{x1D705}\unicode[STIX]{x1D705}[2\mathit{E}(\unicode[STIX]{x1D705})-\mathit{K}(\unicode[STIX]{x1D705})]^{2}}{(1-\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D700}\unicode[STIX]{x1D705})^{7/2}\mathit{K}(\unicode[STIX]{x1D705})}+\int _{0}^{1}\frac{\text{d}\mathit{kk}[2\mathit{E}(\mathit{k})-(2-\mathit{k}^{2})\mathit{K}(\mathit{k})]^{2}}{[(1-\unicode[STIX]{x1D700})\mathit{k}^{2}+2\unicode[STIX]{x1D700}]^{7/2}\mathit{K}(\mathit{k})}\right\}\nonumber\\ \displaystyle & \simeq & \displaystyle \frac{30\sqrt{2}}{\unicode[STIX]{x03C0}}\left\{\int _{0}^{1}\frac{\text{d}\unicode[STIX]{x1D705}\unicode[STIX]{x1D705}}{\mathit{K}(\unicode[STIX]{x1D705})}[2\mathit{E}(\unicode[STIX]{x1D705})-\mathit{K}(\unicode[STIX]{x1D705})]^{2}+\int _{0}^{1}\frac{\text{d}\mathit{k}}{\mathit{k}^{6}\mathit{K}(\mathit{k})}[2\mathit{E}(\mathit{k})-(2-\mathit{k}^{2})\mathit{K}(\mathit{k})]^{2}\right\}\nonumber\\ \displaystyle & \simeq & \displaystyle 4.363.\end{eqnarray}$$Equations (A 65) and (A 66) should read
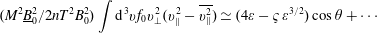 $$\begin{eqnarray}(\mathit{M}^{2}\text{}\underline{\mathit{B}}_{0}^{2}/2\mathit{nT}^{2}\mathit{B}_{0}^{2})\int \text{d}^{3}\mathit{vf}_{0}\mathit{v}_{\bot }^{2}(\mathit{v}_{\Vert }^{2}-\overline{\mathit{v}_{\Vert }^{2}})\simeq (4\unicode[STIX]{x1D700}-\unicode[STIX]{x1D70D}\unicode[STIX]{x1D700}^{3/2})\cos \unicode[STIX]{x1D703}+\cdots\end{eqnarray}$$
$$\begin{eqnarray}(\mathit{M}^{2}\text{}\underline{\mathit{B}}_{0}^{2}/2\mathit{nT}^{2}\mathit{B}_{0}^{2})\int \text{d}^{3}\mathit{vf}_{0}\mathit{v}_{\bot }^{2}(\mathit{v}_{\Vert }^{2}-\overline{\mathit{v}_{\Vert }^{2}})\simeq (4\unicode[STIX]{x1D700}-\unicode[STIX]{x1D70D}\unicode[STIX]{x1D700}^{3/2})\cos \unicode[STIX]{x1D703}+\cdots\end{eqnarray}$$and
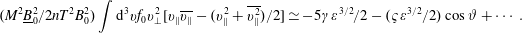 $$\begin{eqnarray}(\mathit{M}^{2}\text{}\underline{\mathit{B}}_{0}^{2}/2\mathit{nT}^{2}\mathit{B}_{0}^{2})\int \text{d}^{3}\mathit{vf}_{0}\mathit{v}_{\bot }^{2}[\mathit{v}_{\Vert }\overline{\mathit{v}_{\Vert }}-(\mathit{v}_{\Vert }^{2}+\overline{\mathit{v}_{\Vert }^{2}})/2]\simeq -5\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D700}^{3/2}/2-(\unicode[STIX]{x1D70D}\unicode[STIX]{x1D700}^{3/2}/2)\cos \unicode[STIX]{x1D717}+\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}(\mathit{M}^{2}\text{}\underline{\mathit{B}}_{0}^{2}/2\mathit{nT}^{2}\mathit{B}_{0}^{2})\int \text{d}^{3}\mathit{vf}_{0}\mathit{v}_{\bot }^{2}[\mathit{v}_{\Vert }\overline{\mathit{v}_{\Vert }}-(\mathit{v}_{\Vert }^{2}+\overline{\mathit{v}_{\Vert }^{2}})/2]\simeq -5\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D700}^{3/2}/2-(\unicode[STIX]{x1D70D}\unicode[STIX]{x1D700}^{3/2}/2)\cos \unicode[STIX]{x1D717}+\cdots \,.\end{eqnarray}$$ Equation (A 71) must be multiplied by 2, so that  $\unicode[STIX]{x1D712}\simeq 0.2262$.
$\unicode[STIX]{x1D712}\simeq 0.2262$.
A more precise evaluation of the  $\cos \unicode[STIX]{x1D717}$ coefficient in (A 80) replaces
$\cos \unicode[STIX]{x1D717}$ coefficient in (A 80) replaces  $\unicode[STIX]{x1D710}=5\unicode[STIX]{x1D6FE}\simeq 8.2$ by
$\unicode[STIX]{x1D710}=5\unicode[STIX]{x1D6FE}\simeq 8.2$ by  $\unicode[STIX]{x1D710}\equiv \unicode[STIX]{x03C0}^{-1}\unicode[STIX]{x1D700}^{-5/2}\oint \text{d}\unicode[STIX]{x1D703}\mathit{I}\cos \unicode[STIX]{x1D717}=7.96$.
$\unicode[STIX]{x1D710}\equiv \unicode[STIX]{x03C0}^{-1}\unicode[STIX]{x1D700}^{-5/2}\oint \text{d}\unicode[STIX]{x1D703}\mathit{I}\cos \unicode[STIX]{x1D717}=7.96$.
This change affects (5.15), (5.19)–(5.21), (5.31), (5.43), (5.45), (6.2), and (6.5)–(6.7). In (5.15), (5.19), (5.31), (5.43), and (6.2), let  $5\unicode[STIX]{x1D6FE}\rightarrow \unicode[STIX]{x1D710}=7.96$. In (5.20) and (5.21), make the replacement
$5\unicode[STIX]{x1D6FE}\rightarrow \unicode[STIX]{x1D710}=7.96$. In (5.20) and (5.21), make the replacement  $1-\unicode[STIX]{x1D700}^{1/2}/2\unicode[STIX]{x1D6FE}\mathit{q}^{2}\rightarrow [(\unicode[STIX]{x1D710}-3\unicode[STIX]{x1D6FE})/2\unicode[STIX]{x1D6FE}][1-(\unicode[STIX]{x1D710}-4\unicode[STIX]{x1D6FE})\unicode[STIX]{x1D700}^{1/2}/(\unicode[STIX]{x1D710}-3\unicode[STIX]{x1D6FE})\mathit{q}^{2}]$. In (6.5) and (6.6), the same replacement gives final forms with
$1-\unicode[STIX]{x1D700}^{1/2}/2\unicode[STIX]{x1D6FE}\mathit{q}^{2}\rightarrow [(\unicode[STIX]{x1D710}-3\unicode[STIX]{x1D6FE})/2\unicode[STIX]{x1D6FE}][1-(\unicode[STIX]{x1D710}-4\unicode[STIX]{x1D6FE})\unicode[STIX]{x1D700}^{1/2}/(\unicode[STIX]{x1D710}-3\unicode[STIX]{x1D6FE})\mathit{q}^{2}]$. In (6.5) and (6.6), the same replacement gives final forms with  $1\rightarrow (\unicode[STIX]{x1D710}-3\unicode[STIX]{x1D6FE})/2\unicode[STIX]{x1D6FE}$. In (5.45), let
$1\rightarrow (\unicode[STIX]{x1D710}-3\unicode[STIX]{x1D6FE})/2\unicode[STIX]{x1D6FE}$. In (5.45), let  $5\unicode[STIX]{x1D6FE}\tilde{\mathit{A}}_{\Vert }^{(0)}\rightarrow \unicode[STIX]{x1D710}\tilde{\mathit{A}}_{\Vert }^{(0)}$ and
$5\unicode[STIX]{x1D6FE}\tilde{\mathit{A}}_{\Vert }^{(0)}\rightarrow \unicode[STIX]{x1D710}\tilde{\mathit{A}}_{\Vert }^{(0)}$ and  $5\unicode[STIX]{x1D6FE}\tilde{\unicode[STIX]{x1D6F7}}^{(0)}\rightarrow [\unicode[STIX]{x1D710}(\unicode[STIX]{x1D710}-3\unicode[STIX]{x1D6FE})/2\unicode[STIX]{x1D6FE}]\tilde{\unicode[STIX]{x1D6F7}}^{(0)}$, while in (6.2) let
$5\unicode[STIX]{x1D6FE}\tilde{\unicode[STIX]{x1D6F7}}^{(0)}\rightarrow [\unicode[STIX]{x1D710}(\unicode[STIX]{x1D710}-3\unicode[STIX]{x1D6FE})/2\unicode[STIX]{x1D6FE}]\tilde{\unicode[STIX]{x1D6F7}}^{(0)}$, while in (6.2) let  $5\unicode[STIX]{x1D6FE}\rightarrow \unicode[STIX]{x1D710}(\unicode[STIX]{x1D710}-3\unicode[STIX]{x1D6FE})/2\unicode[STIX]{x1D6FE}$.
$5\unicode[STIX]{x1D6FE}\rightarrow \unicode[STIX]{x1D710}(\unicode[STIX]{x1D710}-3\unicode[STIX]{x1D6FE})/2\unicode[STIX]{x1D6FE}$.
3 Kinetic equation and solution
Two lines above (3.8),  $\unicode[STIX]{x1D6E5}_{\mathit{s}}$ should be
$\unicode[STIX]{x1D6E5}_{\mathit{s}}$ should be  $\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }$, so the result reads
$\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }$, so the result reads  $\mathit{B}_{\mathit{p}}/\mathit{B}_{\mathit{t}}=(\unicode[STIX]{x1D700}/\mathit{q})[1-\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }\cos \unicode[STIX]{x1D717}+\mathit{O}(\unicode[STIX]{x1D700}^{2})]$.
$\mathit{B}_{\mathit{p}}/\mathit{B}_{\mathit{t}}=(\unicode[STIX]{x1D700}/\mathit{q})[1-\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }\cos \unicode[STIX]{x1D717}+\mathit{O}(\unicode[STIX]{x1D700}^{2})]$.
5 Quasineutrality and Ampere’s law
Remove the last sentence of the paragraph ending after (5.9).
The left side of (5.10) and the beginning of the paragraph including it should read as follows. Expanding for  $\mathit{Q}=\mathit{k}_{\bot }\mathit{v}_{\Vert }/\unicode[STIX]{x1D6FA}_{\mathit{p}}\ll 1$, inserting
$\mathit{Q}=\mathit{k}_{\bot }\mathit{v}_{\Vert }/\unicode[STIX]{x1D6FA}_{\mathit{p}}\ll 1$, inserting  $H$, and neglecting
$H$, and neglecting  $\unicode[STIX]{x1D700}$ corrections to
$\unicode[STIX]{x1D700}$ corrections to  $\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{i}}^{2}$ terms, but retaining all
$\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{i}}^{2}$ terms, but retaining all  $\mathit{Q}^{2}$,
$\mathit{Q}^{2}$,  $\unicode[STIX]{x1D6FD}$, and
$\unicode[STIX]{x1D6FD}$, and  $\unicode[STIX]{x1D700}^{3/2}$ corrections to the
$\unicode[STIX]{x1D700}^{3/2}$ corrections to the  $\tilde{\mathit{B}}_{\Vert }$ and
$\tilde{\mathit{B}}_{\Vert }$ and  $\tilde{\mathit{B}}_{\Vert }^{(0)}$ terms in (5.5), recalling
$\tilde{\mathit{B}}_{\Vert }^{(0)}$ terms in (5.5), recalling  $\tilde{\unicode[STIX]{x1D6F7}}=\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle$, and using unperturbed quasineutrality, the perpendicular Ampere’s law becomes
$\tilde{\unicode[STIX]{x1D6F7}}=\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle$, and using unperturbed quasineutrality, the perpendicular Ampere’s law becomes
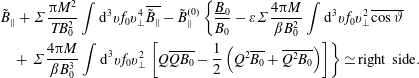 $$\begin{eqnarray}\displaystyle & & \displaystyle \tilde{\mathit{B}}_{\Vert }+\unicode[STIX]{x1D6F4}\frac{\unicode[STIX]{x03C0}\mathit{M}^{2}}{\mathit{TB}_{0}^{2}}\int \text{d}^{3}\mathit{vf}_{0}\mathit{v}_{\bot }^{4}\overline{\tilde{\mathit{B}}_{\Vert }}-\tilde{\mathit{B}}_{\Vert }^{(0)}\left\{\frac{\text{}\underline{\mathit{B}}_{0}}{\mathit{B}_{0}}-\unicode[STIX]{x1D700}\unicode[STIX]{x1D6F4}\frac{4\unicode[STIX]{x03C0}\mathit{M}}{\unicode[STIX]{x1D6FD}\mathit{B}_{0}^{2}}\int \text{d}^{3}\mathit{vf}_{0}\mathit{v}_{\bot }^{2}\overline{\cos \unicode[STIX]{x1D717}}\right.\nonumber\\ \displaystyle & & \displaystyle \quad +\left.\unicode[STIX]{x1D6F4}\frac{4\unicode[STIX]{x03C0}\mathit{ M}}{\unicode[STIX]{x1D6FD}\mathit{B}_{0}^{3}}\int \text{d}^{3}\mathit{vf}_{0}\mathit{v}_{\bot }^{2}\left[\mathit{Q}\overline{\mathit{QB}_{0}}-\frac{1}{2}\left(\mathit{Q}^{2}\overline{\mathit{B}_{0}}+\overline{\mathit{Q}^{2}\mathit{B}_{0}}\right)\right]\right\}\simeq \text{right side}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \tilde{\mathit{B}}_{\Vert }+\unicode[STIX]{x1D6F4}\frac{\unicode[STIX]{x03C0}\mathit{M}^{2}}{\mathit{TB}_{0}^{2}}\int \text{d}^{3}\mathit{vf}_{0}\mathit{v}_{\bot }^{4}\overline{\tilde{\mathit{B}}_{\Vert }}-\tilde{\mathit{B}}_{\Vert }^{(0)}\left\{\frac{\text{}\underline{\mathit{B}}_{0}}{\mathit{B}_{0}}-\unicode[STIX]{x1D700}\unicode[STIX]{x1D6F4}\frac{4\unicode[STIX]{x03C0}\mathit{M}}{\unicode[STIX]{x1D6FD}\mathit{B}_{0}^{2}}\int \text{d}^{3}\mathit{vf}_{0}\mathit{v}_{\bot }^{2}\overline{\cos \unicode[STIX]{x1D717}}\right.\nonumber\\ \displaystyle & & \displaystyle \quad +\left.\unicode[STIX]{x1D6F4}\frac{4\unicode[STIX]{x03C0}\mathit{ M}}{\unicode[STIX]{x1D6FD}\mathit{B}_{0}^{3}}\int \text{d}^{3}\mathit{vf}_{0}\mathit{v}_{\bot }^{2}\left[\mathit{Q}\overline{\mathit{QB}_{0}}-\frac{1}{2}\left(\mathit{Q}^{2}\overline{\mathit{B}_{0}}+\overline{\mathit{Q}^{2}\mathit{B}_{0}}\right)\right]\right\}\simeq \text{right side}.\qquad\end{eqnarray}$$ In the  $\tilde{\mathit{B}}_{\Vert }^{(0)}/\unicode[STIX]{x1D6FD}$ term of (5.11), the factor
$\tilde{\mathit{B}}_{\Vert }^{(0)}/\unicode[STIX]{x1D6FD}$ term of (5.11), the factor  $\overline{\mathit{v}_{\Vert }}-\mathit{v}_{\Vert }$ should be replaced by
$\overline{\mathit{v}_{\Vert }}-\mathit{v}_{\Vert }$ should be replaced by  $\overline{\mathit{v}_{\Vert }}-\mathit{B}_{0}^{-1}\mathit{v}_{\Vert }\overline{\mathit{B}_{0}}$ and in the last term we use
$\overline{\mathit{v}_{\Vert }}-\mathit{B}_{0}^{-1}\mathit{v}_{\Vert }\overline{\mathit{B}_{0}}$ and in the last term we use  $\int \text{d}^{3}\mathit{vf}_{0}\mathit{v}_{\Vert }(\mathit{Q}-\overline{\mathit{Q}})(\mathit{Mv}^{2}/2\mathit{T}-3/2)=\int \text{d}^{3}\mathit{vf}_{0}\mathit{v}_{\Vert }(\mathit{Q}-\overline{\mathit{Q}})$.
$\int \text{d}^{3}\mathit{vf}_{0}\mathit{v}_{\Vert }(\mathit{Q}-\overline{\mathit{Q}})(\mathit{Mv}^{2}/2\mathit{T}-3/2)=\int \text{d}^{3}\mathit{vf}_{0}\mathit{v}_{\Vert }(\mathit{Q}-\overline{\mathit{Q}})$.
Correct the ‘ $a$’ term on the right side of (5.12) by the replacement
$a$’ term on the right side of (5.12) by the replacement  $3\unicode[STIX]{x1D700}\mathit{a}/2\rightarrow 3\mathit{a}/2$ and then fix the left side of (5.12) by keeping
$3\unicode[STIX]{x1D700}\mathit{a}/2\rightarrow 3\mathit{a}/2$ and then fix the left side of (5.12) by keeping  $\unicode[STIX]{x1D6FD}_{\mathit{i}}$ and
$\unicode[STIX]{x1D6FD}_{\mathit{i}}$ and  $\unicode[STIX]{x1D6FD}$ corrections to read
$\unicode[STIX]{x1D6FD}$ corrections to read
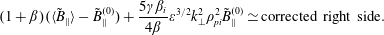 $$\begin{eqnarray}(1+\unicode[STIX]{x1D6FD})(\langle \tilde{\mathit{B}}_{\Vert }\rangle -\tilde{\mathit{B}}_{\Vert }^{(0)})+\frac{5\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D700}^{3/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}\tilde{\mathit{B}}_{\Vert }^{(0)}\simeq \text{corrected right side}.\end{eqnarray}$$
$$\begin{eqnarray}(1+\unicode[STIX]{x1D6FD})(\langle \tilde{\mathit{B}}_{\Vert }\rangle -\tilde{\mathit{B}}_{\Vert }^{(0)})+\frac{5\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D700}^{3/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}\tilde{\mathit{B}}_{\Vert }^{(0)}\simeq \text{corrected right side}.\end{eqnarray}$$Remove the last sentence of the paragraph that ends after (5.12).
In (5.13), remove the  $\mathit{a}\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }$ term on the left side and on the right remove the term proportional to
$\mathit{a}\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }$ term on the left side and on the right remove the term proportional to  $\unicode[STIX]{x1D6FD}_{\mathit{i}}\unicode[STIX]{x1D700}(\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle -\tilde{\unicode[STIX]{x1D6F7}}^{(0)})$ and other
$\unicode[STIX]{x1D6FD}_{\mathit{i}}\unicode[STIX]{x1D700}(\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle -\tilde{\unicode[STIX]{x1D6F7}}^{(0)})$ and other  $\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle$ and
$\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle$ and  $\tilde{\unicode[STIX]{x1D6F7}}^{(0)}$ terms that are negligible in what follows, to obtain
$\tilde{\unicode[STIX]{x1D6F7}}^{(0)}$ terms that are negligible in what follows, to obtain
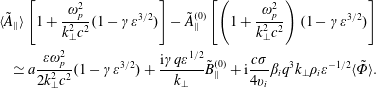 $$\begin{eqnarray}\displaystyle & & \displaystyle \langle \tilde{\mathit{A}}_{\Vert }\rangle \left[1+\frac{\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}{\mathit{k}_{\bot }^{2}\mathit{c}^{2}}(1-\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D700}^{3/2})\right]-\tilde{\mathit{A}}_{\Vert }^{(0)}\left[\left(1+\frac{\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}{\mathit{k}_{\bot }^{2}\mathit{c}^{2}}\right)(1-\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D700}^{3/2})\right]\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \mathit{a}\frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}{2\mathit{k}_{\bot }^{2}\mathit{c}^{2}}(1-\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D700}^{3/2})+\frac{\text{i}\unicode[STIX]{x1D6FE}\mathit{q}\unicode[STIX]{x1D700}^{1/2}}{\mathit{k}_{\bot }}\tilde{\mathit{B}}_{\Vert }^{(0)}+\text{i}\frac{\mathit{c}\unicode[STIX]{x1D70E}}{4\mathit{v }_{\mathit{i}}}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{q}^{3}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}\unicode[STIX]{x1D700}^{-1/2}\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \langle \tilde{\mathit{A}}_{\Vert }\rangle \left[1+\frac{\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}{\mathit{k}_{\bot }^{2}\mathit{c}^{2}}(1-\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D700}^{3/2})\right]-\tilde{\mathit{A}}_{\Vert }^{(0)}\left[\left(1+\frac{\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}{\mathit{k}_{\bot }^{2}\mathit{c}^{2}}\right)(1-\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D700}^{3/2})\right]\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \mathit{a}\frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}{2\mathit{k}_{\bot }^{2}\mathit{c}^{2}}(1-\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D700}^{3/2})+\frac{\text{i}\unicode[STIX]{x1D6FE}\mathit{q}\unicode[STIX]{x1D700}^{1/2}}{\mathit{k}_{\bot }}\tilde{\mathit{B}}_{\Vert }^{(0)}+\text{i}\frac{\mathit{c}\unicode[STIX]{x1D70E}}{4\mathit{v }_{\mathit{i}}}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{q}^{3}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}\unicode[STIX]{x1D700}^{-1/2}\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle .\end{eqnarray}$$ In (5.14), make the replacements  $\mathit{a}\unicode[STIX]{x1D712}\unicode[STIX]{x1D700}^{3/2}\rightarrow \mathit{a}\unicode[STIX]{x1D712}\unicode[STIX]{x1D700}^{1/2}$ and
$\mathit{a}\unicode[STIX]{x1D712}\unicode[STIX]{x1D700}^{3/2}\rightarrow \mathit{a}\unicode[STIX]{x1D712}\unicode[STIX]{x1D700}^{1/2}$ and  $\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle \rightarrow \langle \tilde{\unicode[STIX]{x1D6F7}}\rangle /2$ and fix the
$\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle \rightarrow \langle \tilde{\unicode[STIX]{x1D6F7}}\rangle /2$ and fix the  $\tilde{\mathit{B}}_{\Vert }^{(0)}$ and ‘
$\tilde{\mathit{B}}_{\Vert }^{(0)}$ and ‘ $b$’ terms to read
$b$’ terms to read
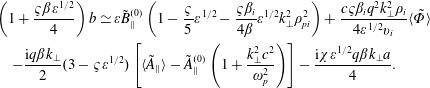 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(1+\frac{\unicode[STIX]{x1D70D}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}}{4}\right)\mathit{b}\simeq \unicode[STIX]{x1D700}\tilde{\mathit{B}}_{\Vert }^{(0)}\left(1-\frac{\unicode[STIX]{x1D70D}}{5}\unicode[STIX]{x1D700}^{1/2}-\frac{\unicode[STIX]{x1D70D}\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D700}^{1/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}\right)+\frac{\mathit{c}\unicode[STIX]{x1D70D}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{q}^{2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{i}}}{4\unicode[STIX]{x1D700}^{1/2}\mathit{v}_{\mathit{i}}}\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle \nonumber\\ \displaystyle & & \displaystyle \quad -\frac{\text{i}\mathit{q}\unicode[STIX]{x1D6FD}\mathit{k}_{\bot }}{2}(3-\unicode[STIX]{x1D70D}\unicode[STIX]{x1D700}^{1/2})\left[\langle \tilde{\mathit{A}}_{\Vert }\rangle -\tilde{\mathit{A}}_{\Vert }^{(0)}\left(1+\frac{\mathit{k}_{\bot }^{2}\mathit{c}^{2}}{\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}\right)\right]-\frac{\text{i}\unicode[STIX]{x1D712}\unicode[STIX]{x1D700}^{1/2}\mathit{q}\unicode[STIX]{x1D6FD}\mathit{k}_{\bot }\mathit{a}}{4}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(1+\frac{\unicode[STIX]{x1D70D}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}}{4}\right)\mathit{b}\simeq \unicode[STIX]{x1D700}\tilde{\mathit{B}}_{\Vert }^{(0)}\left(1-\frac{\unicode[STIX]{x1D70D}}{5}\unicode[STIX]{x1D700}^{1/2}-\frac{\unicode[STIX]{x1D70D}\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D700}^{1/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}\right)+\frac{\mathit{c}\unicode[STIX]{x1D70D}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{q}^{2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{i}}}{4\unicode[STIX]{x1D700}^{1/2}\mathit{v}_{\mathit{i}}}\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle \nonumber\\ \displaystyle & & \displaystyle \quad -\frac{\text{i}\mathit{q}\unicode[STIX]{x1D6FD}\mathit{k}_{\bot }}{2}(3-\unicode[STIX]{x1D70D}\unicode[STIX]{x1D700}^{1/2})\left[\langle \tilde{\mathit{A}}_{\Vert }\rangle -\tilde{\mathit{A}}_{\Vert }^{(0)}\left(1+\frac{\mathit{k}_{\bot }^{2}\mathit{c}^{2}}{\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}\right)\right]-\frac{\text{i}\unicode[STIX]{x1D712}\unicode[STIX]{x1D700}^{1/2}\mathit{q}\unicode[STIX]{x1D6FD}\mathit{k}_{\bot }\mathit{a}}{4}.\end{eqnarray}$$ Following (5.14), correct the constants to read  $\unicode[STIX]{x1D712}\simeq 0.226$ and
$\unicode[STIX]{x1D712}\simeq 0.226$ and  $\unicode[STIX]{x1D70D}\simeq 4.36$.
$\unicode[STIX]{x1D70D}\simeq 4.36$.
Correcting (5.15), because  $\mathit{k}_{\bot }^{2}$ in (4.11) must be a flux function, whereas on the left side of (5.4)
$\mathit{k}_{\bot }^{2}$ in (4.11) must be a flux function, whereas on the left side of (5.4)  $\mathit{k}_{\bot }^{2}\rightarrow \mathit{k}_{\bot }^{2}(1+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }\cos \unicode[STIX]{x1D717})$, and multiplying the
$\mathit{k}_{\bot }^{2}\rightarrow \mathit{k}_{\bot }^{2}(1+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }\cos \unicode[STIX]{x1D717})$, and multiplying the  $\tilde{\mathit{B}}_{\Vert }^{(0)}$ term by 2 gives
$\tilde{\mathit{B}}_{\Vert }^{(0)}$ term by 2 gives
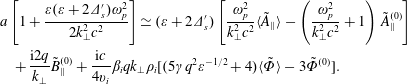 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathit{a}\left[1+\frac{\unicode[STIX]{x1D700}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}{2\mathit{k}_{\bot }^{2}\mathit{c}^{2}}\right]\simeq (\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\left[\frac{\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}{\mathit{k}_{\bot }^{2}\mathit{c}^{2}}\langle \tilde{\mathit{A}}_{\Vert }\rangle -\left(\frac{\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}{\mathit{k}_{\bot }^{2}\mathit{c}^{2}}+1\right)\tilde{\mathit{A}}_{\Vert }^{(0)}\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\text{i}2\mathit{q}}{\mathit{k}_{\bot }}\tilde{\mathit{B}}_{\Vert }^{(0)}+\frac{\text{i}\mathit{c}}{4\mathit{v }_{\mathit{i}}}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{qk}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}[(5\unicode[STIX]{x1D6FE}\mathit{q}^{2}\unicode[STIX]{x1D700}^{-1/2}+4)\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle -3\tilde{\unicode[STIX]{x1D6F7}}^{(0)}].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathit{a}\left[1+\frac{\unicode[STIX]{x1D700}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}{2\mathit{k}_{\bot }^{2}\mathit{c}^{2}}\right]\simeq (\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\left[\frac{\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}{\mathit{k}_{\bot }^{2}\mathit{c}^{2}}\langle \tilde{\mathit{A}}_{\Vert }\rangle -\left(\frac{\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}{\mathit{k}_{\bot }^{2}\mathit{c}^{2}}+1\right)\tilde{\mathit{A}}_{\Vert }^{(0)}\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\text{i}2\mathit{q}}{\mathit{k}_{\bot }}\tilde{\mathit{B}}_{\Vert }^{(0)}+\frac{\text{i}\mathit{c}}{4\mathit{v }_{\mathit{i}}}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{qk}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}[(5\unicode[STIX]{x1D6FE}\mathit{q}^{2}\unicode[STIX]{x1D700}^{-1/2}+4)\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle -3\tilde{\unicode[STIX]{x1D6F7}}^{(0)}].\end{eqnarray}$$ Equations (5.16) and (5.17) are the same as (5.15) and (5.13), but with the  $\tilde{\mathit{B}}_{\Vert }^{(0)}$ terms removed.
$\tilde{\mathit{B}}_{\Vert }^{(0)}$ terms removed.
The large skin depth limit of (5.16) and (5.17) are
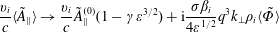 $$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\langle \tilde{\mathit{A}}_{\Vert }\rangle \rightarrow \frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\tilde{\mathit{A}}_{\Vert }^{(0)}(1-\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D700}^{3/2})+\text{i}\frac{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4\unicode[STIX]{x1D700}^{1/2}}\mathit{q}^{3}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\langle \tilde{\mathit{A}}_{\Vert }\rangle \rightarrow \frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\tilde{\mathit{A}}_{\Vert }^{(0)}(1-\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D700}^{3/2})+\text{i}\frac{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4\unicode[STIX]{x1D700}^{1/2}}\mathit{q}^{3}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle\end{eqnarray}$$and
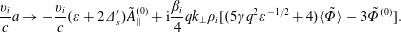 $$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\mathit{a}\rightarrow -\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\tilde{\mathit{A}}_{\Vert }^{(0)}+\text{i}\frac{\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4}\mathit{qk}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}[(5\unicode[STIX]{x1D6FE}\mathit{q}^{2}\unicode[STIX]{x1D700}^{-1/2}+4)\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle -3\tilde{\unicode[STIX]{x1D6F7}}^{(0)}].\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\mathit{a}\rightarrow -\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\tilde{\mathit{A}}_{\Vert }^{(0)}+\text{i}\frac{\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4}\mathit{qk}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}[(5\unicode[STIX]{x1D6FE}\mathit{q}^{2}\unicode[STIX]{x1D700}^{-1/2}+4)\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle -3\tilde{\unicode[STIX]{x1D6F7}}^{(0)}].\end{eqnarray}$$ The small skin depth limits ( $\mathit{k}_{\bot }^{2}\mathit{c}^{2}/\unicode[STIX]{x1D714}_{\mathit{p}}^{2}\ll 1$) of (5.16) and (5.17), (5.20) and (5.21), should read
$\mathit{k}_{\bot }^{2}\mathit{c}^{2}/\unicode[STIX]{x1D714}_{\mathit{p}}^{2}\ll 1$) of (5.16) and (5.17), (5.20) and (5.21), should read
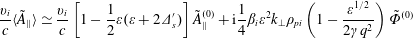 $$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\langle \tilde{\mathit{A}}_{\Vert }\rangle \simeq \frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\left[1-\frac{1}{2}\unicode[STIX]{x1D700}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\right]\tilde{\mathit{A}}_{\Vert }^{(0)}+\text{i}\frac{1}{4}\unicode[STIX]{x1D6FD}_{\mathit{i}}\unicode[STIX]{x1D700}^{2}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\left(1-\frac{\unicode[STIX]{x1D700}^{1/2}}{2\unicode[STIX]{x1D6FE}\mathit{q}^{2}}\right)\tilde{\unicode[STIX]{x1D6F7}}^{(0)}\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\langle \tilde{\mathit{A}}_{\Vert }\rangle \simeq \frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\left[1-\frac{1}{2}\unicode[STIX]{x1D700}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\right]\tilde{\mathit{A}}_{\Vert }^{(0)}+\text{i}\frac{1}{4}\unicode[STIX]{x1D6FD}_{\mathit{i}}\unicode[STIX]{x1D700}^{2}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\left(1-\frac{\unicode[STIX]{x1D700}^{1/2}}{2\unicode[STIX]{x1D6FE}\mathit{q}^{2}}\right)\tilde{\unicode[STIX]{x1D6F7}}^{(0)}\end{eqnarray}$$and
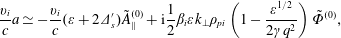 $$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\mathit{a}\simeq -\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\tilde{\mathit{A}}_{\Vert }^{(0)}+\text{i}\frac{1}{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\unicode[STIX]{x1D700}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\left(1-\frac{\unicode[STIX]{x1D700}^{1/2}}{2\unicode[STIX]{x1D6FE}\mathit{q}^{2}}\right)\tilde{\unicode[STIX]{x1D6F7}}^{(0)},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\mathit{a}\simeq -\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\tilde{\mathit{A}}_{\Vert }^{(0)}+\text{i}\frac{1}{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\unicode[STIX]{x1D700}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\left(1-\frac{\unicode[STIX]{x1D700}^{1/2}}{2\unicode[STIX]{x1D6FE}\mathit{q}^{2}}\right)\tilde{\unicode[STIX]{x1D6F7}}^{(0)},\end{eqnarray}$$ upon using (5.9) to calculate the response to  $\tilde{\unicode[STIX]{x1D6F7}}^{(0)}$, because the corrections to
$\tilde{\unicode[STIX]{x1D6F7}}^{(0)}$, because the corrections to  $\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle$ due to
$\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle$ due to  $\tilde{\mathit{A}}_{\Vert }^{(0)}$ are negligible (as will be found from quasineutrality shortly). Notice that at small skin depth the relation
$\tilde{\mathit{A}}_{\Vert }^{(0)}$ are negligible (as will be found from quasineutrality shortly). Notice that at small skin depth the relation  $\langle \tilde{\mathit{A}}_{\Vert }\rangle \simeq \tilde{\mathit{A}}_{\Vert }^{(0)}+\unicode[STIX]{x1D700}\mathit{a}/2$ holds. Keeping
$\langle \tilde{\mathit{A}}_{\Vert }\rangle \simeq \tilde{\mathit{A}}_{\Vert }^{(0)}+\unicode[STIX]{x1D700}\mathit{a}/2$ holds. Keeping  $\unicode[STIX]{x1D700}^{1/2}$ corrections, we note that for
$\unicode[STIX]{x1D700}^{1/2}$ corrections, we note that for  $\tilde{\mathit{A}}_{\Vert }^{(0)}=0$ stronger poloidal variation occurs, as
$\tilde{\mathit{A}}_{\Vert }^{(0)}=0$ stronger poloidal variation occurs, as  $\langle \tilde{\mathit{A}}_{\Vert }\rangle /\mathit{a}\simeq \unicode[STIX]{x1D700}/2$.
$\langle \tilde{\mathit{A}}_{\Vert }\rangle /\mathit{a}\simeq \unicode[STIX]{x1D700}/2$.
Correcting the full parallel Ampere’s law without inserting (5.9), but otherwise making the changes already noted, (5.22) and (5.23) are the same as the corrected (5.15) and (5.13).
Evaluating (5.12) and (5.14) without inserting (5.9), (5.24) and (5.25) should read as follows:
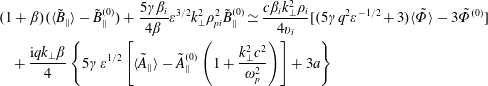 $$\begin{eqnarray}\displaystyle & & \displaystyle (1+\unicode[STIX]{x1D6FD})(\langle \tilde{\mathit{B}}_{\Vert }\rangle -\tilde{\mathit{B}}_{\Vert }^{(0)})+\frac{5\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D700}^{3/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}\tilde{\mathit{B}}_{\Vert }^{(0)}\simeq \frac{\mathit{c}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{i}}}{4\mathit{v}_{\mathit{i}}}[(5\unicode[STIX]{x1D6FE}\mathit{q}^{2}\unicode[STIX]{x1D700}^{-1/2}+3)\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle -3\tilde{\unicode[STIX]{x1D6F7}}^{(0)}]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\text{i}\mathit{qk}_{\bot }\unicode[STIX]{x1D6FD}}{4}\left\{5\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D700}^{1/2}\left[\langle \tilde{\mathit{A}}_{\Vert }\rangle -\tilde{\mathit{A}}_{\Vert }^{(0)}\left(1+\frac{\mathit{k}_{\bot }^{2}\mathit{c}^{2}}{\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}\right)\right]+3\mathit{a}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (1+\unicode[STIX]{x1D6FD})(\langle \tilde{\mathit{B}}_{\Vert }\rangle -\tilde{\mathit{B}}_{\Vert }^{(0)})+\frac{5\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D700}^{3/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}\tilde{\mathit{B}}_{\Vert }^{(0)}\simeq \frac{\mathit{c}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{i}}}{4\mathit{v}_{\mathit{i}}}[(5\unicode[STIX]{x1D6FE}\mathit{q}^{2}\unicode[STIX]{x1D700}^{-1/2}+3)\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle -3\tilde{\unicode[STIX]{x1D6F7}}^{(0)}]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\text{i}\mathit{qk}_{\bot }\unicode[STIX]{x1D6FD}}{4}\left\{5\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D700}^{1/2}\left[\langle \tilde{\mathit{A}}_{\Vert }\rangle -\tilde{\mathit{A}}_{\Vert }^{(0)}\left(1+\frac{\mathit{k}_{\bot }^{2}\mathit{c}^{2}}{\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}\right)\right]+3\mathit{a}\right\}\end{eqnarray}$$and
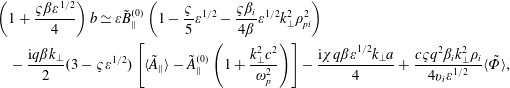 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(1+\frac{\unicode[STIX]{x1D70D}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}}{4}\right)\mathit{b}\simeq \unicode[STIX]{x1D700}\tilde{\mathit{B}}_{\Vert }^{(0)}\left(1-\frac{\unicode[STIX]{x1D70D}}{5}\unicode[STIX]{x1D700}^{1/2}-\frac{\unicode[STIX]{x1D70D}\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D700}^{1/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\text{i}\mathit{q}\unicode[STIX]{x1D6FD}\mathit{k}_{\bot }}{2}(3-\unicode[STIX]{x1D70D}\unicode[STIX]{x1D700}^{1/2})\left[\langle \tilde{\mathit{A}}_{\Vert }\rangle -\tilde{\mathit{A}}_{\Vert }^{(0)}\left(1+\frac{\mathit{k}_{\bot }^{2}\mathit{c}^{2}}{\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}\right)\right]-\frac{\text{i}\unicode[STIX]{x1D712}q\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}\mathit{k}_{\bot }\mathit{a}}{4}+\frac{c\unicode[STIX]{x1D70D}q^{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{i}}}{4\mathit{v}_{\mathit{i}}\unicode[STIX]{x1D700}^{1/2}}\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle ,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(1+\frac{\unicode[STIX]{x1D70D}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}}{4}\right)\mathit{b}\simeq \unicode[STIX]{x1D700}\tilde{\mathit{B}}_{\Vert }^{(0)}\left(1-\frac{\unicode[STIX]{x1D70D}}{5}\unicode[STIX]{x1D700}^{1/2}-\frac{\unicode[STIX]{x1D70D}\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D700}^{1/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\text{i}\mathit{q}\unicode[STIX]{x1D6FD}\mathit{k}_{\bot }}{2}(3-\unicode[STIX]{x1D70D}\unicode[STIX]{x1D700}^{1/2})\left[\langle \tilde{\mathit{A}}_{\Vert }\rangle -\tilde{\mathit{A}}_{\Vert }^{(0)}\left(1+\frac{\mathit{k}_{\bot }^{2}\mathit{c}^{2}}{\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}\right)\right]-\frac{\text{i}\unicode[STIX]{x1D712}q\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}\mathit{k}_{\bot }\mathit{a}}{4}+\frac{c\unicode[STIX]{x1D70D}q^{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{i}}}{4\mathit{v}_{\mathit{i}}\unicode[STIX]{x1D700}^{1/2}}\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle ,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$ where all  $\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle$ and
$\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle$ and  $\tilde{\unicode[STIX]{x1D6F7}}^{(0)}$ terms are corrected. The line following (5.25) and (5.26) should be deleted and replaced by the following sentence. Equations (5.22) and (5.23) are only consistent with
$\tilde{\unicode[STIX]{x1D6F7}}^{(0)}$ terms are corrected. The line following (5.25) and (5.26) should be deleted and replaced by the following sentence. Equations (5.22) and (5.23) are only consistent with
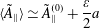 $$\begin{eqnarray}\langle \tilde{\mathit{A}}_{\Vert }\rangle \simeq \tilde{\mathit{A}}_{\Vert }^{(0)}+\frac{\unicode[STIX]{x1D700}}{2}\mathit{a}\end{eqnarray}$$
$$\begin{eqnarray}\langle \tilde{\mathit{A}}_{\Vert }\rangle \simeq \tilde{\mathit{A}}_{\Vert }^{(0)}+\frac{\unicode[STIX]{x1D700}}{2}\mathit{a}\end{eqnarray}$$ in the small skin depth limit, for which field lines switch between irrational and rational when  $\mathit{q}_{1}=\mathit{ik}_{\bot }\mathit{B}_{\mathit{p}}^{-1}\tilde{\mathit{A}}_{\Vert }^{(0)}\neq 0$.
$\mathit{q}_{1}=\mathit{ik}_{\bot }\mathit{B}_{\mathit{p}}^{-1}\tilde{\mathit{A}}_{\Vert }^{(0)}\neq 0$.
When  $\tilde{\mathit{B}}_{\Vert }^{(0)}=0$, the
$\tilde{\mathit{B}}_{\Vert }^{(0)}=0$, the  $\unicode[STIX]{x1D714}_{\mathit{p}}^{2}/\mathit{k}_{\bot }^{2}\mathit{c}^{2}\rightarrow 0$ limits of (5.24) and (5.25) correct (5.27) and (5.28) to read
$\unicode[STIX]{x1D714}_{\mathit{p}}^{2}/\mathit{k}_{\bot }^{2}\mathit{c}^{2}\rightarrow 0$ limits of (5.24) and (5.25) correct (5.27) and (5.28) to read
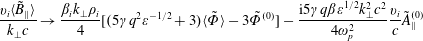 $$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}\langle \tilde{\mathit{B}}_{\Vert }\rangle }{\mathit{k}_{\bot }\mathit{c}}\rightarrow \frac{\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}}{4}[(5\unicode[STIX]{x1D6FE}\mathit{q}^{2}\unicode[STIX]{x1D700}^{-1/2}+3)\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle -3\tilde{\unicode[STIX]{x1D6F7}}^{(0)}]-\frac{\text{i}5\unicode[STIX]{x1D6FE}q\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}\mathit{k}_{\bot }^{2}\mathit{c}^{2}}{4\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\tilde{\mathit{A}}_{\Vert }^{(0)}\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}\langle \tilde{\mathit{B}}_{\Vert }\rangle }{\mathit{k}_{\bot }\mathit{c}}\rightarrow \frac{\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}}{4}[(5\unicode[STIX]{x1D6FE}\mathit{q}^{2}\unicode[STIX]{x1D700}^{-1/2}+3)\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle -3\tilde{\unicode[STIX]{x1D6F7}}^{(0)}]-\frac{\text{i}5\unicode[STIX]{x1D6FE}q\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}\mathit{k}_{\bot }^{2}\mathit{c}^{2}}{4\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\tilde{\mathit{A}}_{\Vert }^{(0)}\end{eqnarray}$$and
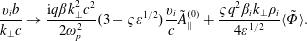 $$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}\mathit{b}}{\mathit{k}_{\bot }\mathit{c}}\rightarrow \frac{\text{i}q\unicode[STIX]{x1D6FD}k_{\bot }^{2}\mathit{c}^{2}}{2\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}(3-\unicode[STIX]{x1D70D}\unicode[STIX]{x1D700}^{1/2})\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\tilde{\mathit{A}}_{\Vert }^{(0)}+\frac{\unicode[STIX]{x1D70D}\mathit{q}^{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}}{4\unicode[STIX]{x1D700}^{1/2}}\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}\mathit{b}}{\mathit{k}_{\bot }\mathit{c}}\rightarrow \frac{\text{i}q\unicode[STIX]{x1D6FD}k_{\bot }^{2}\mathit{c}^{2}}{2\unicode[STIX]{x1D714}_{\mathit{p}}^{2}}(3-\unicode[STIX]{x1D70D}\unicode[STIX]{x1D700}^{1/2})\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\tilde{\mathit{A}}_{\Vert }^{(0)}+\frac{\unicode[STIX]{x1D70D}\mathit{q}^{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}}{4\unicode[STIX]{x1D700}^{1/2}}\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle .\end{eqnarray}$$ The sentences that follow should then read as follows. Consequently, when  $\tilde{\unicode[STIX]{x1D6F7}}^{(0)}=0$, we see that the ratio of the
$\tilde{\unicode[STIX]{x1D6F7}}^{(0)}=0$, we see that the ratio of the  $\tilde{\mathit{A}}_{\Vert }^{(0)}$ terms gives
$\tilde{\mathit{A}}_{\Vert }^{(0)}$ terms gives  $\mathit{b}/\langle \tilde{\mathit{B}}_{\Vert }\rangle \simeq -6/5\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D700}^{1/2}$, so rather strong poloidal variation occurs in
$\mathit{b}/\langle \tilde{\mathit{B}}_{\Vert }\rangle \simeq -6/5\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D700}^{1/2}$, so rather strong poloidal variation occurs in  $\tilde{\mathit{B}}_{\Vert }$. For
$\tilde{\mathit{B}}_{\Vert }$. For  $\tilde{\mathit{A}}_{\Vert }^{(0)}=0$, the poloidal variation of
$\tilde{\mathit{A}}_{\Vert }^{(0)}=0$, the poloidal variation of  $\tilde{\mathit{B}}_{\Vert }$ is strong since
$\tilde{\mathit{B}}_{\Vert }$ is strong since  $\mathit{b}/\langle \tilde{\mathit{B}}_{\Vert }\rangle \simeq \unicode[STIX]{x1D70D}/2\unicode[STIX]{x1D6FE}\simeq 1.3$.
$\mathit{b}/\langle \tilde{\mathit{B}}_{\Vert }\rangle \simeq \unicode[STIX]{x1D70D}/2\unicode[STIX]{x1D6FE}\simeq 1.3$.
For  $\tilde{\mathit{B}}_{\Vert }^{(0)}=0$ and
$\tilde{\mathit{B}}_{\Vert }^{(0)}=0$ and  $\unicode[STIX]{x1D6FD}\ll 1$, the small skin depth (
$\unicode[STIX]{x1D6FD}\ll 1$, the small skin depth ( $\unicode[STIX]{x1D714}_{\mathit{p}}^{2}/\mathit{k}_{\bot }^{2}\mathit{c}^{2}\gg 1$) limits of (5.24) and (5.25) yield the corrected (5.29) and (5.30) to be
$\unicode[STIX]{x1D714}_{\mathit{p}}^{2}/\mathit{k}_{\bot }^{2}\mathit{c}^{2}\gg 1$) limits of (5.24) and (5.25) yield the corrected (5.29) and (5.30) to be
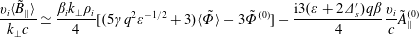 $$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}\langle \tilde{\mathit{B}}_{\Vert }\rangle }{\mathit{k}_{\bot }\mathit{c}}\simeq \frac{\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}}{4}[(5\unicode[STIX]{x1D6FE}\mathit{q}^{2}\unicode[STIX]{x1D700}^{-1/2}+3)\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle -3\tilde{\unicode[STIX]{x1D6F7}}^{(0)}]-\frac{\text{i}3(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })q\unicode[STIX]{x1D6FD}}{4}\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\tilde{\mathit{A}}_{\Vert }^{(0)}\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}\langle \tilde{\mathit{B}}_{\Vert }\rangle }{\mathit{k}_{\bot }\mathit{c}}\simeq \frac{\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}}{4}[(5\unicode[STIX]{x1D6FE}\mathit{q}^{2}\unicode[STIX]{x1D700}^{-1/2}+3)\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle -3\tilde{\unicode[STIX]{x1D6F7}}^{(0)}]-\frac{\text{i}3(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })q\unicode[STIX]{x1D6FD}}{4}\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\tilde{\mathit{A}}_{\Vert }^{(0)}\end{eqnarray}$$and
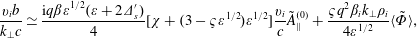 $$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}\mathit{b}}{\mathit{k}_{\bot }\mathit{c}}\simeq \frac{\text{i}q\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })}{4}[\unicode[STIX]{x1D712}+(3-\unicode[STIX]{x1D70D}\unicode[STIX]{x1D700}^{1/2})\unicode[STIX]{x1D700}^{1/2}]\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\tilde{\mathit{A}}_{\Vert }^{(0)}+\frac{\unicode[STIX]{x1D70D}\mathit{q}^{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}}{4\unicode[STIX]{x1D700}^{1/2}}\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathit{v}_{\mathit{i}}\mathit{b}}{\mathit{k}_{\bot }\mathit{c}}\simeq \frac{\text{i}q\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })}{4}[\unicode[STIX]{x1D712}+(3-\unicode[STIX]{x1D70D}\unicode[STIX]{x1D700}^{1/2})\unicode[STIX]{x1D700}^{1/2}]\frac{\mathit{v}_{\mathit{i}}}{\mathit{c}}\tilde{\mathit{A}}_{\Vert }^{(0)}+\frac{\unicode[STIX]{x1D70D}\mathit{q}^{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}}{4\unicode[STIX]{x1D700}^{1/2}}\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle ,\end{eqnarray}$$ where we assume  $\unicode[STIX]{x1D700}^{3/2}\gg \mathit{k}_{\bot }^{2}\mathit{c}^{2}/\unicode[STIX]{x1D714}_{\mathit{p}}^{2}\gg \unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }\unicode[STIX]{x1D700}^{5/2}$. The three sentences that follow should be replaced by the following two sentences. When
$\unicode[STIX]{x1D700}^{3/2}\gg \mathit{k}_{\bot }^{2}\mathit{c}^{2}/\unicode[STIX]{x1D714}_{\mathit{p}}^{2}\gg \unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }\unicode[STIX]{x1D700}^{5/2}$. The three sentences that follow should be replaced by the following two sentences. When  $\tilde{\mathit{A}}_{\Vert }^{(0)}=0$, the poloidal variation of
$\tilde{\mathit{A}}_{\Vert }^{(0)}=0$, the poloidal variation of  $\tilde{\mathit{B}}_{\Vert }$ is strong with
$\tilde{\mathit{B}}_{\Vert }$ is strong with  $\mathit{b}/\langle \tilde{\mathit{B}}_{\Vert }\rangle \simeq \unicode[STIX]{x1D70D}/2\unicode[STIX]{x1D6FE}\,\simeq 1.33$. For
$\mathit{b}/\langle \tilde{\mathit{B}}_{\Vert }\rangle \simeq \unicode[STIX]{x1D70D}/2\unicode[STIX]{x1D6FE}\,\simeq 1.33$. For  $\tilde{\unicode[STIX]{x1D6F7}}^{(0)}=0$, it is also rather strong, since
$\tilde{\unicode[STIX]{x1D6F7}}^{(0)}=0$, it is also rather strong, since  $\mathit{b}/\langle \tilde{\mathit{B}}_{\Vert }\rangle \simeq \unicode[STIX]{x1D712}\unicode[STIX]{x1D700}^{1/2}/3$.
$\mathit{b}/\langle \tilde{\mathit{B}}_{\Vert }\rangle \simeq \unicode[STIX]{x1D712}\unicode[STIX]{x1D700}^{1/2}/3$.
The sentence including (5.31)–(5.32) should be corrected to read as follows. Keeping  $\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle$ terms, the
$\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle$ terms, the  $\unicode[STIX]{x1D714}_{\mathit{p}}^{2}/\mathit{k}_{\bot }^{2}\mathit{c}^{2}\rightarrow 0$ limit gives
$\unicode[STIX]{x1D714}_{\mathit{p}}^{2}/\mathit{k}_{\bot }^{2}\mathit{c}^{2}\rightarrow 0$ limit gives
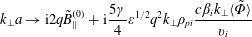 $$\begin{eqnarray}\mathit{k}_{\bot }\mathit{a}\rightarrow \text{i}2\mathit{q}\tilde{\mathit{B}}_{\Vert }^{(0)}+\text{i}\frac{5\unicode[STIX]{x1D6FE}}{4}\unicode[STIX]{x1D700}^{1/2}\mathit{q}^{2}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\frac{\mathit{c}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle }{\mathit{v}_{\mathit{i}}}\end{eqnarray}$$
$$\begin{eqnarray}\mathit{k}_{\bot }\mathit{a}\rightarrow \text{i}2\mathit{q}\tilde{\mathit{B}}_{\Vert }^{(0)}+\text{i}\frac{5\unicode[STIX]{x1D6FE}}{4}\unicode[STIX]{x1D700}^{1/2}\mathit{q}^{2}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\frac{\mathit{c}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle }{\mathit{v}_{\mathit{i}}}\end{eqnarray}$$and
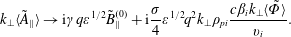 $$\begin{eqnarray}\mathit{k}_{\bot }\langle \tilde{\mathit{A}}_{\Vert }\rangle \rightarrow \text{i}\unicode[STIX]{x1D6FE}q\unicode[STIX]{x1D700}^{1/2}\tilde{\mathit{B}}_{\Vert }^{(0)}+\text{i}\frac{\unicode[STIX]{x1D70E}}{4}\unicode[STIX]{x1D700}^{1/2}\mathit{q}^{2}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\frac{\mathit{c}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle }{\mathit{v}_{\mathit{i}}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathit{k}_{\bot }\langle \tilde{\mathit{A}}_{\Vert }\rangle \rightarrow \text{i}\unicode[STIX]{x1D6FE}q\unicode[STIX]{x1D700}^{1/2}\tilde{\mathit{B}}_{\Vert }^{(0)}+\text{i}\frac{\unicode[STIX]{x1D70E}}{4}\unicode[STIX]{x1D700}^{1/2}\mathit{q}^{2}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\frac{\mathit{c}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle }{\mathit{v}_{\mathit{i}}}.\end{eqnarray}$$Evaluating (5.12) and (5.14) without inserting (5.9), (5.33) and (5.34) should read as follows:
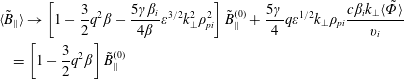 $$\begin{eqnarray}\displaystyle & & \displaystyle \langle \tilde{\mathit{B}}_{\Vert }\rangle \rightarrow \left[1-\frac{3}{2}\mathit{q}^{2}\unicode[STIX]{x1D6FD}-\frac{5\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D700}^{3/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}\right]\tilde{\mathit{B}}_{\Vert }^{(0)}+\frac{5\unicode[STIX]{x1D6FE}}{4}\mathit{q}\unicode[STIX]{x1D700}^{1/2}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\frac{\mathit{c}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle }{\mathit{v}_{\mathit{i}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left[1-\frac{3}{2}\mathit{q}^{2}\unicode[STIX]{x1D6FD}\right]\tilde{\mathit{B}}_{\Vert }^{(0)}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \langle \tilde{\mathit{B}}_{\Vert }\rangle \rightarrow \left[1-\frac{3}{2}\mathit{q}^{2}\unicode[STIX]{x1D6FD}-\frac{5\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D700}^{3/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}\right]\tilde{\mathit{B}}_{\Vert }^{(0)}+\frac{5\unicode[STIX]{x1D6FE}}{4}\mathit{q}\unicode[STIX]{x1D700}^{1/2}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\frac{\mathit{c}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle }{\mathit{v}_{\mathit{i}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left[1-\frac{3}{2}\mathit{q}^{2}\unicode[STIX]{x1D6FD}\right]\tilde{\mathit{B}}_{\Vert }^{(0)}\end{eqnarray}$$and
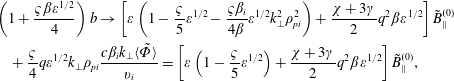 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(1+\frac{\unicode[STIX]{x1D70D}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}}{4}\right)\mathit{b}\rightarrow \left[\unicode[STIX]{x1D700}\left(1-\frac{\unicode[STIX]{x1D70D}}{5}\unicode[STIX]{x1D700}^{1/2}-\frac{\unicode[STIX]{x1D70D}\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D700}^{1/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}\right)+\frac{\unicode[STIX]{x1D712}+3\unicode[STIX]{x1D6FE}}{2}\mathit{q}^{2}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}\right]\tilde{\mathit{B}}_{\Vert }^{(0)}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x1D70D}}{4}\mathit{q}\unicode[STIX]{x1D700}^{1/2}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\frac{\mathit{c}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle }{\mathit{v}_{\mathit{i}}}=\left[\unicode[STIX]{x1D700}\left(1-\frac{\unicode[STIX]{x1D70D}}{5}\unicode[STIX]{x1D700}^{1/2}\right)+\frac{\unicode[STIX]{x1D712}+3\unicode[STIX]{x1D6FE}}{2}\mathit{q}^{2}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}\right]\tilde{\mathit{B}}_{\Vert }^{(0)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(1+\frac{\unicode[STIX]{x1D70D}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}}{4}\right)\mathit{b}\rightarrow \left[\unicode[STIX]{x1D700}\left(1-\frac{\unicode[STIX]{x1D70D}}{5}\unicode[STIX]{x1D700}^{1/2}-\frac{\unicode[STIX]{x1D70D}\unicode[STIX]{x1D6FD}_{\mathit{i}}}{4\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D700}^{1/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}\right)+\frac{\unicode[STIX]{x1D712}+3\unicode[STIX]{x1D6FE}}{2}\mathit{q}^{2}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}\right]\tilde{\mathit{B}}_{\Vert }^{(0)}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\unicode[STIX]{x1D70D}}{4}\mathit{q}\unicode[STIX]{x1D700}^{1/2}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\frac{\mathit{c}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle }{\mathit{v}_{\mathit{i}}}=\left[\unicode[STIX]{x1D700}\left(1-\frac{\unicode[STIX]{x1D70D}}{5}\unicode[STIX]{x1D700}^{1/2}\right)+\frac{\unicode[STIX]{x1D712}+3\unicode[STIX]{x1D6FE}}{2}\mathit{q}^{2}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}\right]\tilde{\mathit{B}}_{\Vert }^{(0)},\end{eqnarray}$$ where  $c\unicode[STIX]{x1D6FD}k_{\bot }\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle /\mathit{v}_{\mathit{i}}\tilde{\mathit{B}}_{\Vert }^{(0)}\simeq \mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}$ is inserted as this result will be determined from quasineutrality in the next subsection, and the
$c\unicode[STIX]{x1D6FD}k_{\bot }\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle /\mathit{v}_{\mathit{i}}\tilde{\mathit{B}}_{\Vert }^{(0)}\simeq \mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}$ is inserted as this result will be determined from quasineutrality in the next subsection, and the  $\unicode[STIX]{x1D6FD}$ correction on the left side is small in the final form.
$\unicode[STIX]{x1D6FD}$ correction on the left side is small in the final form.
Correcting the next paragraph, it should read as follows. In the small skin depth limit  $\unicode[STIX]{x1D700}^{3/2}\unicode[STIX]{x1D714}_{\mathit{p}}^{2}/\mathit{k}_{\bot }^{2}\mathit{c}^{2}\gtrsim 1\gg \unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }\unicode[STIX]{x1D700}^{5/2}\unicode[STIX]{x1D714}_{\mathit{p}}^{2}/\mathit{k}_{\bot }^{2}\mathit{c}^{2}$ for finite
$\unicode[STIX]{x1D700}^{3/2}\unicode[STIX]{x1D714}_{\mathit{p}}^{2}/\mathit{k}_{\bot }^{2}\mathit{c}^{2}\gtrsim 1\gg \unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }\unicode[STIX]{x1D700}^{5/2}\unicode[STIX]{x1D714}_{\mathit{p}}^{2}/\mathit{k}_{\bot }^{2}\mathit{c}^{2}$ for finite  $\unicode[STIX]{x1D6FD}\ll 1$ and
$\unicode[STIX]{x1D6FD}\ll 1$ and  $\tilde{\unicode[STIX]{x1D6F7}}^{(0)}=0=\tilde{\mathit{A}}_{\Vert }^{(0)}$, we use (5.22) and (5.23) along with the quasineutrality result
$\tilde{\unicode[STIX]{x1D6F7}}^{(0)}=0=\tilde{\mathit{A}}_{\Vert }^{(0)}$, we use (5.22) and (5.23) along with the quasineutrality result  $c\unicode[STIX]{x1D6FD}k_{\bot }\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle /\mathit{v}_{\mathit{i}}\tilde{\mathit{B}}_{\Vert }^{(0)}\simeq \mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}$ to find
$c\unicode[STIX]{x1D6FD}k_{\bot }\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle /\mathit{v}_{\mathit{i}}\tilde{\mathit{B}}_{\Vert }^{(0)}\simeq \mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{i}}$ to find  $\unicode[STIX]{x1D700}a\,\simeq 2\langle \tilde{\mathit{A}}_{\Vert }\rangle$. Then (5.22)–(5.25) give
$\unicode[STIX]{x1D700}a\,\simeq 2\langle \tilde{\mathit{A}}_{\Vert }\rangle$. Then (5.22)–(5.25) give
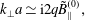 $$\begin{eqnarray}\displaystyle & \mathit{k}_{\bot }\mathit{a}\simeq \text{i}2\mathit{q}\tilde{\mathit{B}}_{\Vert }^{(0)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \mathit{k}_{\bot }\mathit{a}\simeq \text{i}2\mathit{q}\tilde{\mathit{B}}_{\Vert }^{(0)}, & \displaystyle\end{eqnarray}$$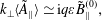 $$\begin{eqnarray}\displaystyle & \mathit{k}_{\bot }\langle \tilde{\mathit{A}}_{\Vert }\rangle \simeq \text{i}q\unicode[STIX]{x1D700}\tilde{\mathit{B}}_{\Vert }^{(0)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \mathit{k}_{\bot }\langle \tilde{\mathit{A}}_{\Vert }\rangle \simeq \text{i}q\unicode[STIX]{x1D700}\tilde{\mathit{B}}_{\Vert }^{(0)}, & \displaystyle\end{eqnarray}$$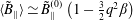 $$\begin{eqnarray}\displaystyle & \langle \tilde{\mathit{B}}_{\Vert }\rangle \simeq \tilde{\mathit{B}}_{\Vert }^{(0)}\left(1-\frac{3}{2}\mathit{q}^{2}\unicode[STIX]{x1D6FD}\right) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \langle \tilde{\mathit{B}}_{\Vert }\rangle \simeq \tilde{\mathit{B}}_{\Vert }^{(0)}\left(1-\frac{3}{2}\mathit{q}^{2}\unicode[STIX]{x1D6FD}\right) & \displaystyle\end{eqnarray}$$and
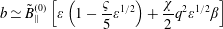 $$\begin{eqnarray}\mathit{b}\simeq \tilde{\mathit{B}}_{\Vert }^{(0)}\left[\unicode[STIX]{x1D700}\left(1-\frac{\unicode[STIX]{x1D70D}}{5}\unicode[STIX]{x1D700}^{1/2}\right)+\frac{\unicode[STIX]{x1D712}}{2}\mathit{q}^{2}\unicode[STIX]{x1D700}^{1/2}\unicode[STIX]{x1D6FD}\right]\end{eqnarray}$$
$$\begin{eqnarray}\mathit{b}\simeq \tilde{\mathit{B}}_{\Vert }^{(0)}\left[\unicode[STIX]{x1D700}\left(1-\frac{\unicode[STIX]{x1D70D}}{5}\unicode[STIX]{x1D700}^{1/2}\right)+\frac{\unicode[STIX]{x1D712}}{2}\mathit{q}^{2}\unicode[STIX]{x1D700}^{1/2}\unicode[STIX]{x1D6FD}\right]\end{eqnarray}$$ for  $\unicode[STIX]{x1D6FD}\sim \unicode[STIX]{x1D700}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}$. As a result, for this
$\unicode[STIX]{x1D6FD}\sim \unicode[STIX]{x1D700}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}$. As a result, for this  $\tilde{\mathit{B}}_{\Vert }^{(0)}\neq 0$ case with
$\tilde{\mathit{B}}_{\Vert }^{(0)}\neq 0$ case with  $\tilde{\unicode[STIX]{x1D6F7}}^{(0)}=0$ and
$\tilde{\unicode[STIX]{x1D6F7}}^{(0)}=0$ and  $\tilde{\mathit{A}}_{\Vert }^{(0)}=0$, the poloidal variation of
$\tilde{\mathit{A}}_{\Vert }^{(0)}=0$, the poloidal variation of  $\tilde{\mathit{A}}_{\Vert }$ is strong with
$\tilde{\mathit{A}}_{\Vert }$ is strong with  $\langle \tilde{\mathit{A}}_{\Vert }\rangle /\mathit{a}\simeq \unicode[STIX]{x1D700}/2$, while the poloidal variation of
$\langle \tilde{\mathit{A}}_{\Vert }\rangle /\mathit{a}\simeq \unicode[STIX]{x1D700}/2$, while the poloidal variation of  $\tilde{\mathit{B}}_{\Vert }$ is weak with
$\tilde{\mathit{B}}_{\Vert }$ is weak with  $\mathit{b}/\langle \tilde{\mathit{B}}_{\Vert }\rangle \simeq \unicode[STIX]{x1D700}$.
$\mathit{b}/\langle \tilde{\mathit{B}}_{\Vert }\rangle \simeq \unicode[STIX]{x1D700}$.
In § 5.4, there are sign errors in the  $\tilde{\mathit{A}}_{\Vert }$ terms of (5.41)–(5.45). The signs can be corrected by changing the signs of all
$\tilde{\mathit{A}}_{\Vert }$ terms of (5.41)–(5.45). The signs can be corrected by changing the signs of all  $\tilde{\mathit{A}}_{\Vert }$,
$\tilde{\mathit{A}}_{\Vert }$,  $\tilde{\mathit{A}}_{\Vert }^{(0)}$,
$\tilde{\mathit{A}}_{\Vert }^{(0)}$,  $\langle \tilde{\mathit{A}}_{\Vert }\rangle$, and ‘
$\langle \tilde{\mathit{A}}_{\Vert }\rangle$, and ‘ $a$’ terms. In addition,
$a$’ terms. In addition,  $5\unicode[STIX]{x1D6FE}/16$ replaces
$5\unicode[STIX]{x1D6FE}/16$ replaces  $(\unicode[STIX]{x1D70E}+5\unicode[STIX]{x1D6FE})/16$ in (5.45) and
$(\unicode[STIX]{x1D70E}+5\unicode[STIX]{x1D6FE})/16$ in (5.45) and  $\unicode[STIX]{x1D700}\rightarrow \unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }$ in the
$\unicode[STIX]{x1D700}\rightarrow \unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }$ in the  $\tilde{\mathit{A}}_{\Vert }^{(0)}$ term, so it becomes
$\tilde{\mathit{A}}_{\Vert }^{(0)}$ term, so it becomes
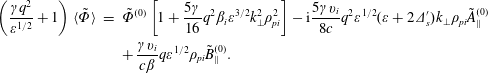 $$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x1D6FE}\mathit{q}^{2}}{\unicode[STIX]{x1D700}^{1/2}}+1\right)\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle & = & \displaystyle \tilde{\unicode[STIX]{x1D6F7}}^{(0)}\left[1+\frac{5\unicode[STIX]{x1D6FE}}{16}\mathit{q}^{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\unicode[STIX]{x1D700}^{3/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}\right]-\text{i}\frac{5\unicode[STIX]{x1D6FE}\mathit{v}_{\mathit{i}}}{8\mathit{c}}\mathit{q}^{2}\unicode[STIX]{x1D700}^{1/2}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\tilde{\mathit{A}}_{\Vert }^{(0)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D6FE}\mathit{v}_{\mathit{i}}}{\mathit{c}\unicode[STIX]{x1D6FD}}\mathit{q}\unicode[STIX]{x1D700}^{1/2}\unicode[STIX]{x1D70C}_{\mathit{pi}}\tilde{\mathit{B}}_{\Vert }^{(0)}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\frac{\unicode[STIX]{x1D6FE}\mathit{q}^{2}}{\unicode[STIX]{x1D700}^{1/2}}+1\right)\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle & = & \displaystyle \tilde{\unicode[STIX]{x1D6F7}}^{(0)}\left[1+\frac{5\unicode[STIX]{x1D6FE}}{16}\mathit{q}^{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\unicode[STIX]{x1D700}^{3/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}\right]-\text{i}\frac{5\unicode[STIX]{x1D6FE}\mathit{v}_{\mathit{i}}}{8\mathit{c}}\mathit{q}^{2}\unicode[STIX]{x1D700}^{1/2}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\tilde{\mathit{A}}_{\Vert }^{(0)}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D6FE}\mathit{v}_{\mathit{i}}}{\mathit{c}\unicode[STIX]{x1D6FD}}\mathit{q}\unicode[STIX]{x1D700}^{1/2}\unicode[STIX]{x1D70C}_{\mathit{pi}}\tilde{\mathit{B}}_{\Vert }^{(0)}.\end{eqnarray}$$6 Zonal flow responses in terms of initial field values: 15 test cases
Section 6 summarizes the small skin depth zonal flow residual responses for the various initial perturbations. The complete summary of the corrected results is as follows.
6.1  $\mathit{A}_{\Vert }^{(0)}=0=\mathit{B}_{\Vert }^{(0)}$
$\mathit{A}_{\Vert }^{(0)}=0=\mathit{B}_{\Vert }^{(0)}$
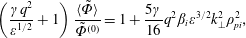 $$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{\unicode[STIX]{x1D6FE}\mathit{q}^{2}}{\unicode[STIX]{x1D700}^{1/2}}+1\right)\frac{\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle }{\tilde{\unicode[STIX]{x1D6F7}}^{(0)}}=1+\frac{5\unicode[STIX]{x1D6FE}}{16}\mathit{q}^{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\unicode[STIX]{x1D700}^{3/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\frac{\unicode[STIX]{x1D6FE}\mathit{q}^{2}}{\unicode[STIX]{x1D700}^{1/2}}+1\right)\frac{\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle }{\tilde{\unicode[STIX]{x1D6F7}}^{(0)}}=1+\frac{5\unicode[STIX]{x1D6FE}}{16}\mathit{q}^{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\unicode[STIX]{x1D700}^{3/2}\mathit{k}_{\bot }^{2}\unicode[STIX]{x1D70C}_{\mathit{pi}}^{2}, & \displaystyle\end{eqnarray}$$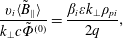 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{v}_{\mathit{i}}\langle \tilde{\mathit{B}}_{\Vert }\rangle }{\mathit{k}_{\bot }\mathit{c}\tilde{\unicode[STIX]{x1D6F7}}^{(0)}}=\frac{\unicode[STIX]{x1D6FD}_{\mathit{i}}\unicode[STIX]{x1D700}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}}{2\mathit{q}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{v}_{\mathit{i}}\langle \tilde{\mathit{B}}_{\Vert }\rangle }{\mathit{k}_{\bot }\mathit{c}\tilde{\unicode[STIX]{x1D6F7}}^{(0)}}=\frac{\unicode[STIX]{x1D6FD}_{\mathit{i}}\unicode[STIX]{x1D700}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}}{2\mathit{q}}, & \displaystyle\end{eqnarray}$$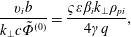 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{v}_{\mathit{i}}\mathit{b}}{\mathit{k}_{\bot }\mathit{c}\tilde{\unicode[STIX]{x1D6F7}}^{(0)}}=\frac{\unicode[STIX]{x1D70D}\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}}{4\unicode[STIX]{x1D6FE}\mathit{q}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{v}_{\mathit{i}}\mathit{b}}{\mathit{k}_{\bot }\mathit{c}\tilde{\unicode[STIX]{x1D6F7}}^{(0)}}=\frac{\unicode[STIX]{x1D70D}\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}}{4\unicode[STIX]{x1D6FE}\mathit{q}}, & \displaystyle\end{eqnarray}$$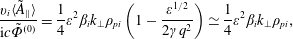 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{v}_{\mathit{i}}\langle \tilde{\mathit{A}}_{\Vert }\rangle }{\text{i}\mathit{c}\tilde{\unicode[STIX]{x1D6F7}}^{(0)}}=\frac{1}{4}\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\left(1-\frac{\unicode[STIX]{x1D700}^{1/2}}{2\unicode[STIX]{x1D6FE}\mathit{q}^{2}}\right)\simeq \frac{1}{4}\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{v}_{\mathit{i}}\langle \tilde{\mathit{A}}_{\Vert }\rangle }{\text{i}\mathit{c}\tilde{\unicode[STIX]{x1D6F7}}^{(0)}}=\frac{1}{4}\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\left(1-\frac{\unicode[STIX]{x1D700}^{1/2}}{2\unicode[STIX]{x1D6FE}\mathit{q}^{2}}\right)\simeq \frac{1}{4}\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}, & \displaystyle\end{eqnarray}$$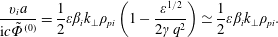 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{v}_{\mathit{i}}\mathit{a}}{\text{i}\mathit{c}\tilde{\unicode[STIX]{x1D6F7}}^{(0)}}=\frac{1}{2}\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\left(1-\frac{\unicode[STIX]{x1D700}^{1/2}}{2\unicode[STIX]{x1D6FE}\mathit{q}^{2}}\right)\simeq \frac{1}{2}\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{v}_{\mathit{i}}\mathit{a}}{\text{i}\mathit{c}\tilde{\unicode[STIX]{x1D6F7}}^{(0)}}=\frac{1}{2}\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}\left(1-\frac{\unicode[STIX]{x1D700}^{1/2}}{2\unicode[STIX]{x1D6FE}\mathit{q}^{2}}\right)\simeq \frac{1}{2}\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FD}_{\mathit{i}}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}. & \displaystyle\end{eqnarray}$$6.2  $\unicode[STIX]{x1D6F7}^{(0)}=0=\mathit{B}_{\Vert }^{(0)}$
$\unicode[STIX]{x1D6F7}^{(0)}=0=\mathit{B}_{\Vert }^{(0)}$
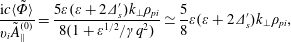 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{i}\mathit{c}\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle }{\mathit{v}_{\mathit{i}}\tilde{\mathit{A}}_{\Vert }^{(0)}}=\frac{5\unicode[STIX]{x1D700}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}}{8(1+\unicode[STIX]{x1D700}^{1/2}/\unicode[STIX]{x1D6FE}\mathit{q}^{2})}\simeq \frac{5}{8}\unicode[STIX]{x1D700}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{i}\mathit{c}\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle }{\mathit{v}_{\mathit{i}}\tilde{\mathit{A}}_{\Vert }^{(0)}}=\frac{5\unicode[STIX]{x1D700}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}}{8(1+\unicode[STIX]{x1D700}^{1/2}/\unicode[STIX]{x1D6FE}\mathit{q}^{2})}\simeq \frac{5}{8}\unicode[STIX]{x1D700}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime })\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}, & \displaystyle\end{eqnarray}$$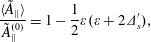 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\langle \tilde{\mathit{A}}_{\Vert }\rangle }{\tilde{\mathit{A}}_{\Vert }^{(0)}}=1-\frac{1}{2}\unicode[STIX]{x1D700}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\langle \tilde{\mathit{A}}_{\Vert }\rangle }{\tilde{\mathit{A}}_{\Vert }^{(0)}}=1-\frac{1}{2}\unicode[STIX]{x1D700}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }), & \displaystyle\end{eqnarray}$$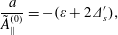 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{a}}{\tilde{\mathit{A}}_{\Vert }^{(0)}}=-(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{a}}{\tilde{\mathit{A}}_{\Vert }^{(0)}}=-(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }), & \displaystyle\end{eqnarray}$$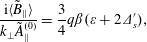 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{i}\langle \tilde{\mathit{B}}_{\Vert }\rangle }{\mathit{k}_{\bot }\tilde{\mathit{A}}_{\Vert }^{(0)}}=\frac{3}{4}\mathit{q}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{i}\langle \tilde{\mathit{B}}_{\Vert }\rangle }{\mathit{k}_{\bot }\tilde{\mathit{A}}_{\Vert }^{(0)}}=\frac{3}{4}\mathit{q}\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }), & \displaystyle\end{eqnarray}$$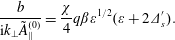 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{b}}{\text{i}\mathit{k}_{\bot }\tilde{\mathit{A}}_{\Vert }^{(0)}}=\frac{\unicode[STIX]{x1D712}}{4}q\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{b}}{\text{i}\mathit{k}_{\bot }\tilde{\mathit{A}}_{\Vert }^{(0)}}=\frac{\unicode[STIX]{x1D712}}{4}q\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D700}^{1/2}(\unicode[STIX]{x1D700}+2\unicode[STIX]{x1D6E5}_{\mathit{s}}^{\prime }). & \displaystyle\end{eqnarray}$$6.3  $\unicode[STIX]{x1D6F7}^{(0)}=0=\mathit{A}_{\Vert }^{(0)}$
$\unicode[STIX]{x1D6F7}^{(0)}=0=\mathit{A}_{\Vert }^{(0)}$
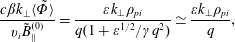 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{c\unicode[STIX]{x1D6FD}k_{\bot }\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle }{\mathit{v}_{\mathit{i}}\tilde{\mathit{B}}_{\Vert }^{(0)}}=\frac{\unicode[STIX]{x1D700}k_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}}{\mathit{q}(1+\unicode[STIX]{x1D700}^{1/2}/\unicode[STIX]{x1D6FE}\mathit{q}^{2})}\simeq \frac{\unicode[STIX]{x1D700}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}}{\mathit{q}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{c\unicode[STIX]{x1D6FD}k_{\bot }\langle \tilde{\unicode[STIX]{x1D6F7}}\rangle }{\mathit{v}_{\mathit{i}}\tilde{\mathit{B}}_{\Vert }^{(0)}}=\frac{\unicode[STIX]{x1D700}k_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}}{\mathit{q}(1+\unicode[STIX]{x1D700}^{1/2}/\unicode[STIX]{x1D6FE}\mathit{q}^{2})}\simeq \frac{\unicode[STIX]{x1D700}\mathit{k}_{\bot }\unicode[STIX]{x1D70C}_{\mathit{pi}}}{\mathit{q}}, & \displaystyle\end{eqnarray}$$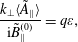 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{k}_{\bot }\langle \tilde{\mathit{A}}_{\Vert }\rangle }{\text{i}\tilde{\mathit{B}}_{\Vert }^{(0)}}=\mathit{q}\unicode[STIX]{x1D700}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{k}_{\bot }\langle \tilde{\mathit{A}}_{\Vert }\rangle }{\text{i}\tilde{\mathit{B}}_{\Vert }^{(0)}}=\mathit{q}\unicode[STIX]{x1D700}, & \displaystyle\end{eqnarray}$$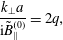 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{k}_{\bot }\mathit{a}}{\text{i}\tilde{\mathit{B}}_{\Vert }^{(0)}}=2\mathit{q}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{k}_{\bot }\mathit{a}}{\text{i}\tilde{\mathit{B}}_{\Vert }^{(0)}}=2\mathit{q}, & \displaystyle\end{eqnarray}$$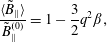 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\langle \tilde{\mathit{B}}_{\Vert }\rangle }{\tilde{\mathit{B}}_{\Vert }^{(0)}}=1-\frac{3}{2}\mathit{q}^{2}\unicode[STIX]{x1D6FD}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\langle \tilde{\mathit{B}}_{\Vert }\rangle }{\tilde{\mathit{B}}_{\Vert }^{(0)}}=1-\frac{3}{2}\mathit{q}^{2}\unicode[STIX]{x1D6FD}, & \displaystyle\end{eqnarray}$$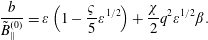 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{b}}{\tilde{\mathit{B}}_{\Vert }^{(0)}}=\unicode[STIX]{x1D700}\left(1-\frac{\unicode[STIX]{x1D70D}}{5}\unicode[STIX]{x1D700}^{1/2}\right)+\frac{\unicode[STIX]{x1D712}}{2}\mathit{q}^{2}\unicode[STIX]{x1D700}^{1/2}\unicode[STIX]{x1D6FD}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\mathit{b}}{\tilde{\mathit{B}}_{\Vert }^{(0)}}=\unicode[STIX]{x1D700}\left(1-\frac{\unicode[STIX]{x1D70D}}{5}\unicode[STIX]{x1D700}^{1/2}\right)+\frac{\unicode[STIX]{x1D712}}{2}\mathit{q}^{2}\unicode[STIX]{x1D700}^{1/2}\unicode[STIX]{x1D6FD}. & \displaystyle\end{eqnarray}$$ All small skin depth results are consistent with  $\langle \tilde{\mathit{A}}_{\Vert }\rangle \simeq \tilde{\mathit{A}}_{\Vert }^{(0)}+\unicode[STIX]{x1D700}\mathit{a}/2$, but field lines can only switch between irrational and rational when
$\langle \tilde{\mathit{A}}_{\Vert }\rangle \simeq \tilde{\mathit{A}}_{\Vert }^{(0)}+\unicode[STIX]{x1D700}\mathit{a}/2$, but field lines can only switch between irrational and rational when  $\mathit{q}_{1}=\text{i}\mathit{k}_{\bot }\mathit{B}_{\mathit{p}}^{-1}\tilde{\mathit{A}}_{\Vert }^{(0)}\neq 0$.
$\mathit{q}_{1}=\text{i}\mathit{k}_{\bot }\mathit{B}_{\mathit{p}}^{-1}\tilde{\mathit{A}}_{\Vert }^{(0)}\neq 0$.
7 Conclusions
The last sentence of the third paragraph from the end should read as follows. The poloidally varying response is larger than the flux surface averaged response for  $\tilde{\mathit{A}}_{\Vert }$ and comparable for
$\tilde{\mathit{A}}_{\Vert }$ and comparable for  $\tilde{\mathit{B}}_{\Vert }$.
$\tilde{\mathit{B}}_{\Vert }$.
In the first sentence of the second paragraph from the end the word ‘also’ should not appear. Replace the last sentence in the same paragraph with the following sentence. However, the poloidal variation of  $\tilde{\mathit{B}}_{\Vert }$ is almost comparable to its flux surface averaged value.
$\tilde{\mathit{B}}_{\Vert }$ is almost comparable to its flux surface averaged value.
Acknowledgements
P.J.C. was supported by the US Department of Energy, grant DE-FG02-91ER-54109. I.P. was supported by an International Career grant (Dnr. 330-2014-631) from Vetenskapsrådet, and the Marie Sklodowska Curie Actions, Cofund, Project INCA 600398. One benefit of having to write this Corrigendum is that it gives us another (and, hopefully, final) chance to thank (and curse) A. Schekochihin of Oxford University for suggesting this problem in March 2013 at a workshop at the Wolfgang Pauli Institute in Vienna, Austria.





