Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-25T03:44:17.894Z Has data issue: false hasContentIssue false
  • English
  • Français

A sub-functor for Ext and Cohen–Macaulay associated graded modules with bounded multiplicity-II

Part of: Commutative algebra: Homological methods Theory of modules and ideals General commutative ring theory

Published online by Cambridge University Press:  30 October 2024

Ankit Mishra Open the ORCID record for Ankit Mishra [Opens in a new window]  and
Tony J. Puthenpurakal
Ankit Mishra*
Affiliation:
Department of Mathematics, GITAM (Deemed to be University), Hyderabad, Telangana, 502329, India
Tony J. Puthenpurakal
Affiliation:
Department of Mathematics, Indian Institute of Technology Bombay, Powai, Mumbai, Maharashtra, 400076, India
*
Corresponding author: Ankit Mishra; Email: chandra.ankit412@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 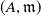$(A,\mathfrak{m})$ be a Cohen–Macaulay local ring, and then the notion of a 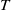$T$-split sequence was introduced in the part-1 of this paper for the 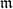$\mathfrak{m}$-adic filtration with the help of the numerical function 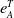$e^T_A$. In this article, we explore the relation between Auslander–Reiten (AR)-sequences and 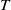$T$-split sequences. For a Gorenstein ring 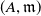$(A,\mathfrak{m})$, we define a Hom-finite Krull–Remak–Schmidt category 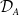$\mathcal{D}_A$ as a quotient of the stable category 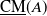$\underline{\mathrm{CM}}(A)$. This category preserves isomorphism, that is, 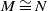$M\cong N$ in 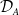$\mathcal{D}_A$ if and only if 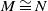$M\cong N$ in 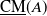$\underline{\mathrm{CM}}(A)$.This article has two objectives: first objective is to extend the notion of 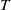$T$-split sequences, and second objective is to explore the function 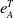$e^T_A$ and 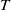$T$-split sequences. When 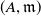$(A,\mathfrak{m})$ is an analytically unramified Cohen–Macaulay local ring and 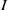$I$ is an 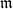$\mathfrak{m}$-primary ideal, then we extend the techniques in part-1 of this paper to the integral closure filtration with respect to 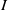$I$ and prove a version of Brauer–Thrall-II for a class of such rings.

MSC classification

Primary: 13A30: Associated graded rings of ideals (Rees ring, form ring), analytic spread and related topics 13C14: Cohen-Macaulay modules
Secondary: 13D40: Hilbert-Samuel and Hilbert-Kunz functions; Poincaré series 13D07: Homological functors on modules (Tor, Ext, etc.)
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 67 , Issue 1 , January 2025 , pp. 86 - 106
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

André, M., Localisation de la lissité formelle, Manuscripta Math. 13(3) (1974), 297–307.CrossRefGoogle Scholar
Atiyah, M. F. and Macdonald, T. G., Introduction to commutative algebra (Addison-Wesley Publishing Co., Reading, Massachusetts, London, Don Mills, Ontario, 1969).Google Scholar
Brennan, J. P., Herzog, J. and Ulrich, B., Maximally generated Cohen-Macaulay modules, Math. Scand. 61(2) (1987), 181–203.CrossRefGoogle Scholar
Bruns, W. and Herzog, J., Cohen-Macaulay rings, Cambridge Studies in Advanced Mathematics, vol. 39 (Cambridge University Press, Cambridge, 1993).Google Scholar
Buchweitz, R.-O., Maximal Cohen-Macaulay modules and Tate cohomology over Gorenstein rings, Mathematical Surveys and Monographs, vol. 262 (American Mathematical Society, Providence, RI, 2021).CrossRefGoogle Scholar
Bühler, T., Exact categories, Expo. Math. 28(1) (2010), 1–69.CrossRefGoogle Scholar
Ciupercă, C., Integral closure and generic elements, J. Algebra 328(1) (2011), 122–131.CrossRefGoogle Scholar
Dao, H., Dey, S. and Dutta, M., Exact subcategories, subfunctors of Ext, and some applications, Nagoya Math. J. 254 (2024), 379–419.CrossRefGoogle Scholar
Dräxler, P., Reiten, I., Smalø, S. O. and Solberg, Ø., Exact categories and vector space categories, (With an appendix by B Keller), Trans. Am. Math. Soc. 351(2) (1999), 647–682.CrossRefGoogle Scholar
Eisenbud, D., Homological algebra on a complete intersection, with an application to group representations, Trans. Am. Math. Soc. 260(1) (1980), 35–64.CrossRefGoogle Scholar
Heinzer, W., Rotthaus, C. and Wiegand, S., Integral closures of ideals in completions of regular local domains, in Commutative algebra (Chapman & Hall/CRC, Boca Raton, FL, 2006), 141–150.Google Scholar
Huneke, C. and Swanson, I., Integral closure of ideals, rings, and modules, London Mathematical Society Lecture Note Series, vol. 336 (Cambridge University Press, Cambridge, 2006).Google Scholar
Kadu, G. S. and Puthenpurakal, T. J., Bass and Betti numbers of $A/I^n$ , J. Algebra 573 (2021), 620–640.CrossRefGoogle Scholar
Matsumura, H., Commutative ring theory, vol. 8, 2nd edition (Cambridge University Press, Cambridge, 1989). translated from the Japanese by M. Reid.Google Scholar
Puthenpurakal, T. J., Hilbert coefficients of a Cohen–Macaulay module, J. Algebra 264(1) (2003), 82–97.CrossRefGoogle Scholar
Puthenpurakal, T. J., The Hilbert function of a maximal Cohen-Macaulay module, Math. Z. 251(3) (2005), 551–573.CrossRefGoogle Scholar
Puthenpurakal, T. J., A function on the set of isomorphism classes in the stable category of maximal Cohen-Macaulay modules over a Gorenstein ring: with applications to liaison theory, Math. Scand. 120(2) (2017), 161–180.CrossRefGoogle Scholar
Puthenpurakal, T. J., Growth of Hilbert coefficients of Syzygy modules, J. Algebra 482 (2017), 131–158.CrossRefGoogle Scholar
Puthenpurakal, T. J., Symmetries and connected components of the AR-quiver of a Gorenstein local ring, Algebr. Represent. Theory 22(5) (2019), 1261–1298.CrossRefGoogle Scholar
Puthenpurakal, T. J., A sub-functor for Ext and Cohen-Macaulay associated graded modules with bounded multiplicity, Trans. AMS 373(4) (2020), 2567–2589.CrossRefGoogle Scholar
Rees, D., A note on analytically unramified local rings, J. Lond. Math. Soc. 36(1) (1961), 24–28.CrossRefGoogle Scholar
Weibel, C. A., An introduction to homological algebra (Cambridge University Press, Cambridge, 1995).Google Scholar
Yoshino, Y., Cohen-Macaulay modules over Cohen-Macaulay rings, London Mathematical Society Lecture Note Series, vol. 146 (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar