1. Introduction
Boreholes in glaciers and ice sheets are drilled for many different purposes. Depending on the drilling technique and depth, a borehole may be filled with water or a drilling fluid of a density equal to ice, or it may be dry. If boreholes can be kept open and accessible for narrow instruments, they allow the time evolution of different quantities related to the dynamics of the ice mass to be logged. Inclinometer measurements give information on the flow field deforming the borehole axis (Reference Hooke, Holmlund and IversonHooke and others, 1987; Reference Hubbard, Blatter, Nienow, Mair and HubbardHubbard and others, 1998). A historical overview of different aspects of inclinometry is given by Reference Blake and ClarkeBlake and Clarke (1992).
The deformation of borehole cross-sections is the result of the local strain field and yields information about the rheological properties of firn and ice (Reference NyeNye, 1953; Reference PatersonPaterson, 1977; Reference Naruse, Okuhira, Ohmae, Kawada and NakawoNaruse and others, 1988; Reference Lüthi and FunkLüthi and Funk, 2000). Repeated measurements of the depth of identifiable marks in boreholes yield the information needed to calculate the profiles of the vertical velocity and strain rate. These marks may be material markers such as metal rings (Reference Hawley, Waddington, Morse, Dunbar and ZielinskiHawley and others, 2002, Reference Hawley, Waddington, Lamorey and Taylor2004), magnetic rings (Reference GudmundssonGudmundsson, 2002), recognizable patterns produced by the drilling (Reference PatersonPaterson, 1976), or they may be devices such as wire strain meters or electronic distance meters with optical fibers installed in the borehole (Reference ZumbergeZumberge and others, 2002).
To log the shape of borehole cross-sections, the most frequently used probes are three-contact-point (arms) caliper probes. This is sufficient to determine closure rates of boreholes with the implicit assumption that circular borehole cross-sections remain circular. To determine an elliptical borehole shape with a caliper probe, five points are necessary. If the caliper can be positioned concentric with the elliptic borehole, three points would be sufficient. However, even with spring-loaded caliper arms, it seems questionable whether the probe in an inclined borehole is truly centered. Five points are required for an exact fit of an ellipse; however, the shape is very sensitive to even the smallest of changes in any of the points. More than five points provide the information for a regression ellipse, which is less sensitive to perturbations.
In this paper, we present an inclinometer–caliper probe with eight arms, together with the mathematical background for the evaluation of elliptic borehole cross-sections. In the next section, the technical aspects of the probe are presented and the mathematical methods for evaluating the caliper measurements are introduced. Possible processes leading to the deformation of borehole cross-sections are discussed in section 3, and in section 4, measurements from two different boreholes from the Swiss Alps (Fiescherhorn and Piz Zupo) are presented, and the proposed methods are tested using the available data.
2. Eight-Arm Caliper-Inclinometer Probe
2.1. Description of the system
The caliper–inclinometer probe was constructed by Intergeo Haferland AG Switzerland, at the request of the glaciology section of ETH-Zürich, Switzerland. The borehole logging system consists of three units: a combined caliper–inclinometer probe, a winch and an electronic interface (Fig. 1). In addition, a portable computer is required to record the data. The probe has a cylindrical shape, is 2 m long, 45 mm in diameter and weighs 12 kg. It is waterproof to a pressure of 2 × 106 Pa and works at ambient temperatures as low as –28°C. The upper end of the probe is connected to a detachable steel cable with two inner conductors. The probe combines three different tools: the eight-arm caliper, an inclinometer and a compass. The expansion of the eight caliper arms is driven by an electric motor. The resistance of eight potentiometers, mechanically coupled to the arms, allows the angle of each arm to be determined. Inside the probe, two crosswise-oriented inclinometers (Hall sensors) measure the tilt of the probe up to 16° from the vertical in all directions with a resolution of 0.1°. A cardanic-bedded compass with jeweled pivot, included in the head of the probe, gives the azimuth of the tilt and the azimuth of the reference caliper arm with a nominal accuracy of 1 °. The temperature of the probe is measured with a thermistor, which provides the information needed to correct thermal shifts. An electronic unit is located in the upper half of the probe. A 16-fold multiplexer converts the signals from the caliper potentiometers, tilt sensors, compass and thermistor by pulse code modulation (PCM) (bidirectional, two-wire code). The 16 values can be recorded approximately two times a second.

Fig. 1. Caliper–inclinometer probe with electronic interface, winch and enlarged view of the expanded arms.
The second unit consists of the winch with a 600 m steel cable and two electric wires inside. It is powered by a 350 W electric motor with 230 V a.c.-rated voltage. The hoisting and lowering speed can be regulated continuously up to a maximum of 50 cm s−1. The rolled-out cable length is recorded electronically by counting the rotations of a measuring wheel with a depth resolution of about 1 cm. With a cross-weight of 52 kg, the winch is the heaviest part of the equipment.
To log the shape of a borehole, the eight arms (Fig. 1) in the lower part of the probe can be extended by an electrical pulse from the interface tool. The 18 cm long arms are arranged radially around the probe and can be extended to an angle of 70° to the probe axis, which limits the measurable radius to 19 cm. They are pushed out by spring tension until they touch the borehole wall (Fig. 2). Each arm is mechanically coupled to an ohmic potentiometer (Fig. 3). The electric resistances of the potentiometers are measured and converted to give the angles of the extended arms.

Fig. 2. Schematic diagram of the expanded arms of the caliper–inclinometer probe in an elliptic borehole (horizontal projection). The local coordinate system (with reference to the probe) is given by x, y and x 0; y 0 indicates the offset of the ellipse center with semimajor and semi-minor axes a and b. The angle between the reference coordinate system and the semi-major ellipse axis is denoted by α.

Fig. 3. Drawing (left side) and photograph (right side) of two of the arms of the caliper–inclinometer probe. The expansion is driven by an electric motor (M), transmitted by a central thread rod and one spring per arm. A second spring (S) per arm pushes them back to the original position. The resistances of eight potentiometers (P), mechanically coupled with the arms, allow the angle of each arm to be determined. In the photograph, one arm is folded and one extended.
The electronic interface monitors the extension of the eight caliper arms, and a control lamp indicates their retracted or extended status. The depth of the probe is displayed in four-digit resolution, relative to an arbitrary resettable zero position. Additionally, this unit connects the probe through an RS232 interface to the recording computer.
To log the hole in one single sounding, the tilt and its azimuth are recorded incrementally at 1 m intervals during the continuous descent of the probe. At the bottom of the hole, the eight arms are extended, and during the continuous ascent the positions of the eight arms and the azimuth of the reference arm are recorded incrementally (e.g. every centimeter (freely adjustable)).
2.2. Calibration
The caliper was calibrated using a reference steel disc. Circular grooves with rectangular cross-section were machined into a steel plate with an accuracy in diameter of ±0.01 mm at 20°C. Calibrations were carried out at temperatures of 0, –5, –10, –15 and –20°C, by putting the eight arms into the grooves with predetermined diameter. The recording of changes in the extension of an arm tends to be stepwise in ~0.5 mm steps during both continuous extending and contracting. This stepping is produced by the discontinuous variation in the ohmic potentiometers, and it limits the resolution of the caliper log to ~0.5 mm.
The inclinometer was calibrated over the same temperature range as it hung under the roof of the cooling room. Each of the five inclinations (0, 5, 10, 15 and 18°) was measured four times while rotating the probe by 90° around its axis. Repeating this procedure for 16 different azimuths led to 320 independent measurements for each temperature. These data yield a standard deviation of 0.13° for the tilt sensors.
Plumbing the depth by counting the revolutions of the sheave is the main source of measurement error, due to the discrepancy between the true cable length and the wheel diameter. The cable diameter on the wheel depends slightly on the cable pressure, cable temperature and possible formation of ice on the wheel or cable. A deviation of 0.01 mm in the effective radius causes an error of about 2 cm at a depth of 100 m. Additional sources of error can be introduced by the potential slip of the cable. Tests conducted by marking the cable itself during a field campaign indicated a relative error in the depth measurement of about 0.025% with a resolution of about 1 cm.
2.3. Regression circle and ellipse
The eight positions of the eight tips of the caliper arms can be determined in a local coordinate system. This permits the approximation of regression circles or ellipses. The general equations for circles and ellipses are long known and are described in detail in many textbooks on analytical geometry (e.g. Reference CaseyCasey, 1893). Here, for convenience, we repeat the basic equations and give some hints for their derivation.
The equation of a circle with radius R and center (x 0, y 0),
can be rewritten in a polynomial form,
with
and
The equation for an ellipse with the semi-major and semiminor axes, a and b, parallel to the coordinate axis and center (0,0) is
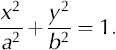
The eccentricity of this ellipse is ![]() Rotation of the coordinate system about an angle α and a translation of the coordinates to shift the center of the ellipse to (x
0, y
0) (Fig. 2) yields an equation of the ellipse in polynomial form,
Rotation of the coordinate system about an angle α and a translation of the coordinates to shift the center of the ellipse to (x
0, y
0) (Fig. 2) yields an equation of the ellipse in polynomial form,
with
and
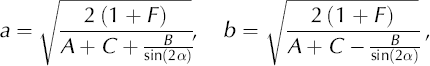
with ![]()
According to Equation (8), B vanishes together with the angle α,

and thus the denominators in Equation (9) are defined in these limits.
Substituting the eight measured points of the caliper, Pi = (xi, yi ) for i = 1, ..., 8, into Equation (2) or (6) yields a system of eight linear equations for the three coefficients in the case of a circle and five in the case of an ellipse,
where ![]() =(A, D, E)T and
=(A, D, E)T and ![]() = (A, B, C, D, E)T are the corresponding vectors of the unknown coefficients for the circle and ellipse, respectively. Furthermore,
= (A, B, C, D, E)T are the corresponding vectors of the unknown coefficients for the circle and ellipse, respectively. Furthermore, ![]() = (1, 1, ..., 1)
T
is a constant vector of length 8, G is the 8 by 3 (3 rows) or 8 by 5 coefficient matrix for a circle or an ellipse, respectively, and
= (1, 1, ..., 1)
T
is a constant vector of length 8, G is the 8 by 3 (3 rows) or 8 by 5 coefficient matrix for a circle or an ellipse, respectively, and ![]() is the vector of length 8 of the residuals. To minimize the sum of the squares of the residuals,
is the vector of length 8 of the residuals. To minimize the sum of the squares of the residuals,

where hk
are the components of ![]() , which yields an equation for the coefficients of the regression circle,
, which yields an equation for the coefficients of the regression circle,
The residuals are calculated by ![]() The distance, di
, of one of the points, Pi
, to the regression ellipse is a function of the corresponding residuum, ri
,
The distance, di
, of one of the points, Pi
, to the regression ellipse is a function of the corresponding residuum, ri
,

For a circle, the same relation holds, but with R = a = b. This approximation of regression circles or ellipses will be used as the hypothetical shape of a deformed borehole.
3. Borehole Deformation
The shape of a borehole changes with time due to the overall flow of the ice and the local borehole closure. The crosssection of the borehole changes both its shape due to horizontal shear and strain, and its area due to lithostatic pressure, vertical strain, vertical shear and change in density. A circular borehole closes isotropically under lithostatic pressure alone or by vertical strain alone, if the flow properties of the ice are horizontally isotropic, and thus remains circular. Vertical strain alone yields a pure divergence in the horizontal plane and thus conserves any shape. Lithostatic pressure alone closes an initially noncircular borehole anisotropically, but it is not clear whether an originally elliptic cross-section will remain elliptic. Pure shearing in the horizontal plane deforms a circular or elliptic borehole cross-section into an elliptic cross-section with equal area.
The combined effect of overall ice flow and closure is difficult to analyze in detail and requires a numerical analysis of the local strain fields. Deviations from elliptic shapes are not observable with the given accuracy of the caliper probe and are thus beyond the scope of this work.
3.1. Pure shear flow
A borehole with circular cross-section deforms into an elliptic cross-section if it is situated in planar pure shear flow in the plane normal to the borehole axis. For planar shear, the gradient of the velocity field is a symmetric tensor of second rank with vanishing trace. Without loss of generality, the off-diagonal elements can be set to zero, which corresponds to a rotation of the coordinate system. In Cartesian coordinates (x, y) in the horizontal plane, such a velocity field is described by

where ε is the strain rate. The differential displacement in a time-step dt is given by the differential equation

which can be integrated by separation of variables. Substituting the solution into the parametric representation of a circle with radius r, where 0 ≤ α ≤ 2π is the polar angle:
yields a parametric representation of an ellipse,
with the semi-major and semi-minor axes a = r exp(εΓt), b = r exp(−εΔt), respectively, Δt the time since the start of shearing of the circular cross-section and strain rate
3.2. Borehole closure
To calculate isotropic borehole closure, we follow the method of Reference NyeNye (1953). The mass-continuity equation written in cylindrical coordinates (r,θ,z) is simplified by assuming cylindrical symmetry, ∂/∂θ = 0 and assuming that the density of the ice is a function of depth, z, alone, so ρ = ρ(z),

where ur and uz are the velocity components in r and z directions, respectively. The third term on the lefthand side, L, can be determined by borehole measurement of the profiles of density and vertical velocity. The solution of Equation (20) is
where K ≤ 0 is an integration constant which depends on the borehole diameter and the lithostatic pressure at a given depth below the ice surface.
In the case of vanishing vertical strain, L ≠ 0, we follow Reference NyeNye (1953) by applying the force-balance equation in cylindrical coordinates with the same symmetries, and Glen’s flow law with the rate factor A Glen and flow law exponent n,
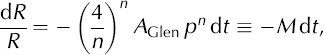
where ρ is the lithostatic pressure. The solution of Equation (22) gives an exponential decay of the radius, R, of the borehole
The closure velocity of the borehole wall is ur (R) = –MR (Equation (22)), and thus the integration constant K = –MR 2 is constant in the entire spatial domain at any time, but varies with time. In the case of non-vanishing vertical strain, L ≠ 0, the radial velocity field is dominated by the divergence far away from the borehole axis, whereas near the borehole axis the velocity due to closure becomes important. Assuming that the borehole radius is small, the simple superposition of the two components of the radial velocity field at the borehole wall renders an initial approximation of the radial velocity of the wall of the borehole,

Thus, depending on the vertical strain, L, the borehole may close or may open. However, the divergence field influences the viscosity of the ice due to the non-linearity of the stress–strain-rate relation for ice, and thus it may influence the closure rate parameter, M.
Non-circular cross-sections of the borehole lead to anisotropic borehole closure. Elliptic borehole shapes may be produced by shear flow in the horizontal plane. To test the hypothesis that elliptic boreholes remain elliptic during the closure due to lithostatic pressure, further analyses are required.
4. Field Measurements
4.1. Study sites
Measurements with the caliper–inclinometer probe were carried out in the accumulation areas of Morteratsch- and Fiescherhorngletscher in the Swiss Alps. The ice cores were drilled by the Paul Scherrer Institute, Villigen, Switzerland, in the context of the project VITA (Varves, Ice cores and Tree rings: Archives with annual resolution) of the Swiss National Center of Competence in Research (NCCR Climate) (Reference Jenk, Gäggeler, Schwerzmann and SchwikowskiJenk and others, 2003; Reference Sodemann, Palmer, Schwierz, Schwikowski and WernliSodemann and others, 2005). Morteratschgletscher is situated between Piz Bernina and Piz Palu in the southeastern Swiss Alps (46°22′ N, 9°56′ E). On a firn saddle next to Piz Zupo, an ice core (PZ02) was drilled in March 2002 at 3853 m a.s.l. to a depth of 43 m. Because of unexpected temperate ice in the middle of the ice body, the bed at an estimated depth of 80 m could not be reached. A second ice core (FH02) was drilled to the bed at 150 m depth on a firn plateau at 3923 m a.s.l. on Fiescherhorngletscher (46°33′ N, 8°04′ E) (Reference SteblerStebler and others, 2004, Reference Stebler, Schwerzmann, Lüthi, Meier and Nüesch2005a, Reference Stebler and Lacosteb) in December 2002.
Immediately after drilling, the drill head was used to scratch grooves into the borehole wall at regular distances down to the bottom of the hole (Fig. 4; for more details see Reference Schwerzmann, Funk, Blatter, Lüthi, Schwikowski and PalmerSchwerzmann and others, 2006). After scratching the marks into the ice, the borehole was logged with the caliper probe to obtain its shape and the depths of the scratched marks on day 0 for reference. Additional complete loggings were carried out 66, 200, 405 and 529 days later on Piz Zupo, and 79 and 179 days later on Fiescherhorn.

Fig. 4. Schematic diagram of the drilling motor scratching the marks into the ice of the borehole wall.
4.2. Vertical strain
The positions of the marks relative to a reference point comoving with the ice at the surface were recorded at all the soundings and are shown for Fiescherhorn in Figure 5 where they are the sharp peaks. The depth difference of the marks indicates the amount of firn compaction and vertical displacement during this period (Reference Schwerzmann, Funk, Blatter, Lüthi, Schwikowski and PalmerSchwerzmann and others, 2006). The right panel of Figure 5 shows the vertical strain rates in the holes PZ02 and FH02 on Piz Zupo and Fiescherhorn.

Fig. 5. Left panel: Diameter of the regression circles of the borehole on Fiescherhorn at days 0, 79 and 179 as a function of depth. The visible tick marks denote the scratched marks in the borehole wall. Right panel: Vertical strain rate determined from positions of the marks in the borehole on Fiescherhorn between days 0 and 179 (solid line), and on Piz Zupo between days 0 and 405 (dash–dotted line).
Changes in layer thicknesses can be determined to an accuracy of ±2.5 × 10−4 times the layer thickness but no smaller than 1 cm, independent of depth. Averaging repeated measurements can reduce this error by ~50%, which enables vertical strain rates as small as 5 × 10−4 a−1 to be determined.
4.3. Borehole shape
In the best case, the inclinometer probe is parallel to the borehole at any given point. Suspended from the steel cable, the probe tends to touch the borehole wall on the inner side at the top and on the outer side at the bottom of the probe (Fig. 6). The angle, β, between the axis of the borehole and the axis of the probe is limited by β « arcsin[(d h – d p)/I], where d h, d p and l are the diameter of the borehole at the corresponding position, the diameter and the length of the probe, respectively. The measurements in the top 50 m of the Fiescherhorn borehole on day 0 show irregular variations with slight inclinations. This seems to be caused by oscillations of the seemingly freely hanging probe during the ascent into the nearly vertical hole.

Fig. 6. Caliper–inclinometer probe situated in a tilted borehole; β indicates the angle between the probe and the borehole at present position, dh describes the borehole diameter, d h the probe diameter and l the probe length.
The borehole tilt and its direction are measured every meter along the entire borehole. Integrating the tilt and its direction along the profile (downwards) yields a threedimensional reconstruction of the hole. The position of the upper border of the hole was determined by means of differential GPS (global positioning system) measurements. Figure 7 shows the projections of borehole FH02 on Fiescherhorn at days 0, 79 and 179 without correction.

Fig. 7. Shapes of the borehole on Fiescherhorn at day 0 (thick line), day 79 (medium line) and day 179 (thin line) based on the inclinometer data. The labels denote a local coordinate system in meters.
The ice at the base of this borehole is not assumed to slide over its bed since ice temperatures are well below freezing point (Reference Schwerzmann, Funk, Blatter, Lüthi, Schwikowski and PalmerSchwerzmann and others, 2006), and thus the bottom of the borehole is not expected to move. However, without correction of tilt, the three computed bottom points lie about 1 m apart, which corresponds to a systematic error in the inclinations of about 0.4°. To improve the reliability of the inclinometry, active control of the position of the probe relative to the direction of the borehole axis is required. This can be done using a spring-loaded mechanism which holds the probe at both ends, centered in the borehole.
4.4. Borehole cross-section
The cross-section of the borehole was measured from the bed to the surface every centimeter. An overview over the computed regression circles and ellipses for hole FH02 on Fiescherhorn at days 0 and 179, and for hole PZ02 on Piz Zupo at days 0, 200 and 405, is shown in Figure 8.

Fig. 8. Circle and ellipse regressions and their residuals on Fiescherhorn at day 0 (thick line) and day 179 (thin line) and Piz Zupo at day 0 (thick line), day 200 (medium line) and day 405 (thin line).
On Fiescherhorn, the borehole closure is clearly shown to increase with depth. At day 0, the residuals for regression circles are small throughout the profile, whereas for day 179, the residuals increase with depth. This may be a result of the slightly increasing eccentricity of the regression ellipses with depth. In the top two-thirds of the hole, no trend in eccentricity is visible. No clear pattern in the directions of the axis of the ellipses is obtained. At eccentricities of less than 0.3, the difference between the axis of the ellipses is less than 5% of the semi-major axis, which is about 2.5 mm. The residuals are about 0.02 in the lowest part, which corresponds to a distance of ±1 mm between the measured points and the regression ellipse. As the regression ellipse has an excess of only three points, the mean residual is expected to be smaller than that for the regression circle with an excess of five points. In this case, one cannot assume an ellipse to be a more advantageous shape than a circle.
The situation is clearer in the case of the caliper sounding on Piz Zupo. The eccentricity systematically increases with time and reaches a value of ~0.6 on day 405. The directions of the axis of the ellipses also remain quite stable over the entire profile after day 200. At an eccentricity of 0.6, the difference between the axis of the ellipses is as much as 20% of the semi-major axis, which is about 10 mm. In this case, regression ellipses are obviously preferable to regression circles.
For day 0, the case on Piz Zupo is similar to the Fiescherhorn borehole. The residuals for the regression circles are similar to the residuals for the regression ellipses. However, we can assume the drilling process produces circular cross-sections rather than ellipses with systematic patterns in eccentricity and directions of the axis. A circular starting shape is also a necessary condition for applying Equation (19) to compute the strain rates in the planar flow field normal to the borehole axis. Equation (19) also requires that the pure strain field is not superposed by additional borehole closure (see Equation (24)). Therefore, an analysis of the strain rate is only feasible for the top 20 m of the borehole, where the closure is small. On days 200 and 405, eccentricities are approximately 0.4–0.42 and 0.58–0.6 at ~15 m depth, which yields strain rates of 0.080–0.088 a−1 and 0.092–0.10 a−1, respectively. Ideally, the values should be equal for both days, but it is not clear to what extent borehole closure or non-zero divergence in the flow field influences the measurements.
5. Conclusions and Prospects
Originally, the measurements presented here were primarily designed for logging borehole closure. The eight arms allow a relatively simple method to be used to determine the borehole shape. For optimal exploitation of the possibilities, careful planning of additional measurements at the surface or in the borehole is crucial. For this reason, some results are presented in this work even though the available information is not sufficient in all cases to confirm the hypothesis that boreholes deform elliptically.
Inclinometry provides the basis for reconstructing the course of the borehole and the horizontal velocity components as a function of depth. Reliable control over the inclination of the borehole can, perhaps, only be achieved by actively controlling the possible angle between the probe axis and the axis of the borehole. This suggests that inclinometry and caliper probing should be done with two different instruments with an inclinometer that is centered on the borehole at both its top and bottom; if the two instruments need to be combined, two sets of caliper arms would be required to reconstruct the inclinometer axis with respect to the borehole axis. In the reported case of Fiescherhorn, where the dislocation of the top of the borehole between the first and last inclinometry was only 2 m, the given accuracy of inclinometry was not good enough to obtain the vertical profile of the longitudinal velocity component.
Scratching identifiable marks into the wall of the borehole allows the vertical dislocation to be tracked, which in turn allows us to determine the vertical strain rates along the borehole. An accurate reference system at the surface and reproducible measurements of the plumbing are crucial for ensuring the accuracy of the measured depths of the marks.
The eight-arm caliper sounding yields the shape of the cross-section of the borehole. Regression circles and ellipses are only the first obvious hypothesis to be tested. Isotropic borehole closure may be expected at dome situations, whereas boreholes situated on inclined glaciers are expected, in addition, to be exposed to anisotropic strain fields. From borehole logging alone, it will not be possible to separate the effects of lithostatic pressure, anisotropic strain and the horizontal divergence resulting from non-zero vertical strain. For this purpose, additional measurements of velocity and strain fields at the ice surface combined with numerical modeling will be required.
Acknowledgements
This study was financially supported by grant No. 0-20948-01 of the Swiss Federal Institute of Technology and the National Center of Competence in Research (NCCR Climate), project VITA (Varves, Ice cores and Tree rings: Archives with annual resolution). We greatly appreciate being able to use the High Alpine Research Station Jungfraujoch as base camp. The caliper–inclinometer probe was constructed by Intergeo Haferland AG, Hunzenschwil, Switzerland, and we gratefully acknowledge their technical support. We thank the Piz Zupo and Fiescherhorn drilling crews for their work under harsh conditions and T. Even and S. Braun-Clark for proofreading.










