1. INTRODUCTION
Collisions in port waters account for a major share of the all port-water accidents involving vessels (Goossens and Glansdorp, Reference Goossens and Glansdorp1998; Akten, Reference Akten2004; Darbra and Casal, Reference Darbra and Casal2004; Yip, Reference Yip2008). A number of researchers (e.g., Debnath and Chin, Reference Debnath and Chin2007; Chin and Debnath, Reference Chin and Debnath2008; Chin et al., Reference Chin, Debnath and Wang2010; Debnath and Chin, Reference Debnath and Chin2010; Weng et al., Reference Weng, Meng and Qu2012) have contended that navigational collisions would remain a major concern for many seaports due to a rapid increase in the numbers and sizes of vessels in many navigational areas (Soares and Teixeira, Reference Guedes Soares and Teixeira2001).
To address this important safety concern in port water navigation, many researchers (e.g., Goossens and Glansdorp, Reference Goossens and Glansdorp1998; Akten, Reference Akten2004; Darbra and Casal, Reference Darbra and Casal2004; Liu et al., Reference Liu, Liang, Su and Chu2006; Yip, Reference Yip2008) have looked at understanding the characteristics and causes of collisions by analysing the historical records of navigational accidents. As an alternative to the historical data, recently some researchers (e.g., Debnath and Chin, Reference Debnath and Chin2006; Debnath and Chin, Reference Debnath and Chin2010; Montewka et al., Reference Montewka, Hinz, Kujala and Matusiak2010; Debnath et al., Reference Debnath, Chin and Haque2011; Weng et al., Reference Weng, Meng and Qu2012; Li et al., Reference Li, Lam and Fan2014) have looked at surrogate indicators of the collision events, such as navigational traffic conflicts and close encounters between vessels.
Apart from the efforts on the analysis of historical collision records and surrogate indicators of collision events, researchers looked at the safety issues related to navigational collisions using a variety of methodological approaches, such as traffic flow-based methods (Montewka et al., Reference Montewka, Goerlandt and Kujala2012; Silveira et al., Reference Silveira, Teixeira and Guedes Soares2013), traffic simulation-based methods (van Dorp and Merrick, Reference van Dorp and Merrick2011; Blokus-Roszkowska and Smolarek, Reference Blokus-Roszkowska and Smolarek2012; Goerlandt et al., Reference Goerlandt, Ståhlberg and Kujala2012), methods using traffic indices (Qu et al., Reference Qu, Meng and Suyi2011; Suman et al., Reference Suman, Nagarajan, Sha, Khanfir, Kobayashi and Malik2012), Bayesian networks (Hänninen et al., Reference Hänninen, Mazaheri, Kujala, Montewka, Laaksonen, Salmiovirta and Klang2013; Montewka et al., Reference Montewka, Ehlers, Goerlandt, Hinz, Tabri and Kujala2014), and fuzzy failure mode and effect analysis methods (Zaman et al., Reference Zaman, Kobayashi, Wakabayashi, Khanfir, Pitana and Maimun2014). The IALA IWrap MKII model (IALA, 2012) presented guidelines for estimating collision frequencies by multiplying the number of collision candidates with causation probability. Burmeister et al. (Reference Burmeister, Walther, Jahn, Tãster and Froese2014) provided a detailed description of the IWrap model in the context of collisions in anchorages. Goerlandt and Kujala (Reference Goerlandt and Kujala2014) reviewed the different methodological approaches for studying ship-ship collisions and found a low inter-method reliability among the approaches, thus highlighting the need for further research on refining the existing methods or developing new methods. Sormunen et al. (Reference Sormunen, Goerlandt, Häkkinen, Posti, Hänninen, Montewka, Ståhlberg and Kujala2014) further discussed the uncertainty of using traffic simulation-based methods and highlighted that simulation methods should be improved for estimating how ship encounter scenarios develop into collision scenarios. Arguably, using real-world traffic movement data for understanding how the encounter scenarios develop into collision scenarios might help in reducing the uncertainty present in traffic simulation models.
A common methodological approach of utilising real-world traffic movement data is the surrogate indicators-based method. The safety analysis approach based on the surrogate indicators of collisions is appealing, because it overcomes the major limitations of the traditional approach that relies on historical collision records. Debnath and Chin (Reference Debnath and Chin2010) have discussed this issue in detail in their article which introduced a novel and proactive approach for measuring the risks of collisions, namely the Navigational Traffic Conflict Technique (NTCT). The NTCT utilises traffic conflicts as an alternative to historical collision records, thus it allows managing collisions in a proactive manner. The major benefit of using NTCT is that safety analysts do not need to wait for years so that a large number of collisions can be accrued—accumulating a large number of collisions might actually not be possible since these collisions are random and sporadic events, and are subjected to continuous changes in waterway conditions and navigational aids—rather preventive or corrective actions can be taken by analysing traffic movements data from a relatively short period of time.
Despite the recent developments in the area of developing proactive safety management techniques, little research has been carried out in applying these techniques for port anchorages. Almost all research efforts (e.g., Debnath and Chin, Reference Debnath and Chin2010; Montewka et al., Reference Montewka, Hinz, Kujala and Matusiak2010; Debnath et al., Reference Debnath, Chin and Haque2011; Weng et al., Reference Weng, Meng and Qu2012) have been devoted so far to examining safety issues related to collisions in fairways and channels. A major part of vessel movements within port waters occur in fairways and channels, which might be why these waters have been a target of considerable research.
Collision statistics from port waters indicate that the likelihood of collision could be high in other parts of port waters, particularly in anchorages. For example, Yip (Reference Yip2008) reported from an analysis of navigational accidents in Hong Kong waters that 20% of collisions occur in anchorages (some of which might include barge traffic), whereas only 10% occur in fairways. Moreover, Liu et al. (Reference Liu, Liang, Su and Chu2006) argued that often vessels anchor arbitrarily in busy seaports. In particular, vessels with a clear departure schedule tend to anchor near boundaries of channels or fairways for easy access. This arbitrary anchoring practice, in combination with a high density of vessels (both anchored and underway) could result in having limited space between vessels, thus creating difficult manoeuvring processes for vessels intending to anchor or to come out of anchorages (Usui, Reference Usui2002). Consequently, these factors might lead to collisions involving moving vessels and anchored vessels. Burmeister et al. (Reference Burmeister, Walther, Jahn, Tãster and Froese2014) argued that anchorages pose risk to navigational safety as anchored vessels might act as obstacles leading to collisions with moving vessels. Proper positioning of anchored vessels has been highlighted as an important technique for avoiding collisions with moving vessels by Zhang and Zhao (Reference Zhang and Zhao2013) who also argued that such collisions are not uncommon in port waters. In summary, relatively little attention has been given to understand the safety issues related to anchorages in port waters, compared to other port waters (e.g., fairways). In a recent study, Burmeister et al. (Reference Burmeister, Walther, Jahn, Tãster and Froese2014) studied collision risks in anchorages using the IALA IWrap MkII model (IALA, 2012). They presented a methodology for extending the use of IWrap model in assessing the frequency and material consequences of collisions between an anchored vessel and a vessel underway. The developed methodology was illustrated using simulated data. While this study marks as a good attempt to estimate collision frequencies in anchorages, further research is required, particularly on 1) using real-world traffic movement data instead of simulated data, and 2) examining the contributing factors of collisions in anchorages.
This paper aims to fill these important gaps in port navigational safety literature by applying the NTCT for measuring collision potentials in anchorages using real-world traffic movement data and for examining the factors contributing to the collisions. Specifically, a proactive Collision Potential Measurement model is developed which provides a quantitative measurement of the collision potentials in anchorages. For examining the effects of contributing factors, a prediction model is developed which examines the relationships between the collision potentials and the geometric, traffic, and regulatory control characteristics of anchorages. Both the measurement and prediction models are illustrated for anchorages within Singapore port waters by using vessel movement data obtained from the Port's Vessel Traffic Information System (VTIS). The rest of the paper discusses the two models first, followed by a description of the data used for illustrating the models. Model calibration and validation results are presented next, before providing concluding remarks.
2. METHOD
2.1. Collision Potential Measurement Model (CPMM)
The NTCT was developed by Debnath and Chin (Reference Debnath and Chin2010) and looks at surrogate indicators of navigational collisions for estimating the collision potentials in waterways. The fundamental principle behind the NTCT methodology is based on the hypothesis that all interactions between vessels fall within a continuum of safety related events (Debnath and Chin, Reference Debnath and Chin2006) with collisions at the top of a hierearchical system. A key feature is that “close proximity” vessel interactions (also known as “collision candidates”) - situations in which two or more vessels are sufficiently close in space and time and whose trajectories will cross unless evasive actions are taken - reside just below collisions in the hierarchy. These interactions are called near-misses, traffic conflicts, or surrogate measures of collision potential. NTCT focuses on these surrogate indicators of collision events in order to derive a quantitative estimate of the probability of collision in a two-vessel interaction or collectively for all interactions within a waterway (i.e., fairway, anchorages).
To estimate the collision potential in an anchorage for a given time period, at first it is necessary to estimate the collision potentials for all two-vessel interactions within the anchorage. Navigational traffic movement is essentially two-dimensional in nature (particularly within anchorage waters where vessels need to navigate through the spaces available between anchored vessels). Therefore, the closeness of two vessels to a potential collision event should be represented both in terms of spatial and temporal closeness. The Distance at Closet Point of Approach (DCPA) and Time to Closest Point of Approach (TCPA) indicators were proposed by Debnath and Chin (Reference Debnath and Chin2010) for representing the spatial and temporal closeness between a pair of vessels. These indicators are widely used in on board navigation and navigational research and thus have general acceptability to navigators and researchers. Research (e.g., Chin and Debnath, Reference Chin and Debnath2009; Debnath and Chin, Reference Debnath and Chin2010) showed that these indicators are well capable of representing the collision potential of an interaction.
To derive the collision potential in a vessel interaction as a function of the DCPA and TCPA, Chin and Debnath (Reference Chin and Debnath2009) developed a set of statistical regression models for different vessel size classes. By employing these models, the collision potential in an interaction can be estimated at short intervals (e.g., 2–5 seconds) throughout the entire interaction process. It should be noted that interactions in which vessels are far away from each other (i.e., a collision is not probable) need to be excluded from this estimation process. The concept of Ship Domain (SD) was proposed as an acceptable criterion for defining which vessels to exclude (see Debnath (Reference Debnath2009) for details). Therefore, the collision potentials were estimated for the interactions where one vessel was within the SD of a vessel that is present in an anchorage (these interactions are termed as ‘encounters’ hereafter). Each vessel in an anchorage was paired with all other vessels within the SD of the vessel in the anchorage and the collision potential for each pair was estimated.
From these estimated collision potentials at different timestamps during an encounter process involving a pair of vessels, the most severe point of the encounter (when the collision potential is the highest) can be identified. Let us take C max as the highest collision potential found in an interaction. Converting C max to ![]() $C_{max}^{\prime} \, = \,\left( {1/\left( {1\, - \,{C_{max}}} \right)} \right)$ and considering all
$C_{max}^{\prime} \, = \,\left( {1/\left( {1\, - \,{C_{max}}} \right)} \right)$ and considering all ![]() $C_{max}^{\prime} $ values within an anchorage, a left-truncated distribution (at
$C_{max}^{\prime} $ values within an anchorage, a left-truncated distribution (at ![]() $C_{max}^{\prime} \, = \,1$) with an asymptotic tail towards right can be obtained. Since
$C_{max}^{\prime} \, = \,1$) with an asymptotic tail towards right can be obtained. Since ![]() $C_{max}^{\prime} $ represents the severity of a conflict in terms of closeness to a collision event (i.e., a higher value indicates more likelihood of collision), the tail of the curve could be utilised to estimate the collision potential in an anchorage by setting a threshold value that will separate the serious conflicts from the non-serious ones. A serious conflict corresponds to vessel encounter that may lead to a certain collision if appropriate evasive actions are not taken urgently. Empirical results from a study (Debnath, Reference Debnath2009), which tested a set of left-truncated distributions to obtain the best-fit distribution, showed that a truncated gamma distribution consistently provides the best fit for the distribution of
$C_{max}^{\prime} $ represents the severity of a conflict in terms of closeness to a collision event (i.e., a higher value indicates more likelihood of collision), the tail of the curve could be utilised to estimate the collision potential in an anchorage by setting a threshold value that will separate the serious conflicts from the non-serious ones. A serious conflict corresponds to vessel encounter that may lead to a certain collision if appropriate evasive actions are not taken urgently. Empirical results from a study (Debnath, Reference Debnath2009), which tested a set of left-truncated distributions to obtain the best-fit distribution, showed that a truncated gamma distribution consistently provides the best fit for the distribution of ![]() $C_{max}^{\prime} $ values. The cumulative distribution function of the truncated gamma distribution can be written as:
$C_{max}^{\prime} $ values. The cumulative distribution function of the truncated gamma distribution can be written as:
 $$\eqalign{{F_{C_{max}^{\prime} }}\left( {C_{max}^{\prime} } \right)\, & = \,p\left( 0 \right)\, + \,\left[ {1\, - \,p\left( 0 \right)\int_\theta ^\tau {\displaystyle{1 \over {{\rm \Gamma \gamma }\, \times \,{{\rm \delta }^\gamma }}}{{\left( {q - \theta } \right)}^{\gamma - 1}}ex{\,p^{\displaystyle{{ - \left( {q - \theta } \right)} \over \delta }}}dq} } \right]}$$
$$\eqalign{{F_{C_{max}^{\prime} }}\left( {C_{max}^{\prime} } \right)\, & = \,p\left( 0 \right)\, + \,\left[ {1\, - \,p\left( 0 \right)\int_\theta ^\tau {\displaystyle{1 \over {{\rm \Gamma \gamma }\, \times \,{{\rm \delta }^\gamma }}}{{\left( {q - \theta } \right)}^{\gamma - 1}}ex{\,p^{\displaystyle{{ - \left( {q - \theta } \right)} \over \delta }}}dq} } \right]}$$where p(0) is a probability mass function which represents the proportions of non-conflict encounters (when two vessels are not likely to collide); τ is a threshold value which distinguishes the serious conflicts from the non-serious ones; γ and δ are the estimated shape and scale parameters of the gamma distribution respectively; and θ is the threshold parameter representing the truncation value (=1).
Since the collision potentials vary with vessel sizes, it is necessary to consider different threshold values (τ) for different vessel classes (vc). Considering p vc as a probability mass function of different vessel classes, the collision potential in an anchorage can be expressed as:
where τ vc is the threshold value for vessel class vc; and M is the total number of vessel classes.
The collision potential (CP) expresses the overall probability of collision in an anchorage in terms of the probability of serious conflict per vessel encounter. Types of collisions in anchorages could be broadly classified into three categories based on the types of vessels involved: 1) collisions between two anchored vessels (including drifting cases), 2) collisions between an anchored vessel and a vessel underway, and 3) collisions between two vessels underway, as defined by Burmeister et al. (Reference Burmeister, Walther, Jahn, Tãster and Froese2014). Since the current study analysed collision potentials of all possible vessel pairs including the anchored vessels and the vessels underway (i.e., all vessels within the SD of a particular vessel in an anchorage), the estimated collision potential in the anchorage was an aggregated value for all collision categories. Separate analyses for each category of collisions were not performed in the current study.
To capture the effects of visibility and presence of navigational aids, the collision potentials should be measured separately for day and night periods.
2.2. Collision Potential Prediction Model (CPPM)
While the CPMM measures the collision potentials in anchorages by analysing the vessel movement trajectories in the anchorages, the CPPM allows predicting the collision potentials by inputting known characteristics of the anchorages in the CPPM. The CPPM establishes relationships between the collision potentials (estimated by the CPMM) and the geometric, traffic, and regulatory control characteristics of anchorages. It models the CP values in each encounter as a dichotomous response variable: serious conflict (=1) and non-serious conflict (=0). Grounding on the modelling framework developed by Debnath et al. (Reference Debnath, Chin and Haque2011), this response variable can effectively be modelled as proportional data (i.e., proportions of serious conflicts among all encounters). A Binomial Logistic Model (BLM) is an ideal choice for modelling such proportional data.
The BLM expresses the occurrence probability of a serious conflict (p eat) for an encounter e at time t in an anchorage a as:
 $$p_{eat} \, = \,E\left( {\displaystyle{{SC_{at}} \over {SC_{at} \, + \,NSC_{at}}}} \right)\, = \,\displaystyle{{{\rm exp}\left( {{\bf \beta X}_{eat}} \right)} \over {1\, + \,{\rm exp}\left( {{\bf \beta X}_{eat}} \right)}}$$
$$p_{eat} \, = \,E\left( {\displaystyle{{SC_{at}} \over {SC_{at} \, + \,NSC_{at}}}} \right)\, = \,\displaystyle{{{\rm exp}\left( {{\bf \beta X}_{eat}} \right)} \over {1\, + \,{\rm exp}\left( {{\bf \beta X}_{eat}} \right)}}$$where Xeat is a vector of explanatory variables representing the geometric, traffic, and regulatory control characteristics of anchorage a; β is a vector of regression coefficients; and SC at and NSC at are the numbers of serious conflicts and non-serious conflicts, respectively, in anchorage a at time t.
3. DATA
The CPMM and CPPM are illustrated by using vessel movement data of the anchorages in Singapore port waters (see Figure 1 for a map which shows nine clusters of anchorages). This data, obtained from the VTIS of the Port, include vessels' trajectories (position coordinates, speeds, headings) and numeric identities. The data fields are generally updated at short intervals (a few seconds) depending on the speeds and density of vessels at the anchorages. Four hours' data from each of day and night periods were used in the illustrative example. Based on the results from existing studies (Debnath and Chin, Reference Debnath and Chin2010; Debnath et al., Reference Debnath, Chin and Haque2011), four hours' data was deemed sufficient for obtaining statistically reliable results.

Figure 1. Anchorages in Singapore port waters (numerically numbered and marked as hatched areas).
A total of 15 explanatory variables, which are hypothesized to relate to the collision potentials in anchorages, were included in the CPPM. The variables were selected based on the existing knowledge from the literature (e.g., Debnath et al., Reference Debnath, Chin and Haque2011; Debnath and Chin, Reference Debnath and Chin2009b), local knowledge regarding the anchorages in the study area and availability of information related to the geometric and traffic characteristics of the anchorages. Among these variables, four were excluded from the model due to multi-collinearity. The definitions of the remaining variables, together with their means and standard deviations (S.D.), are presented in Table 1.
Table 1. Explanatory variables included in the RPM.

Since collision potentials in anchorages are likely to be influenced by traffic in its boundary waters, it is necessary to consider the boundary effects in the CPPM. Therefore, the waters around an anchorage were described in five categories: shoreline, intersection, confined water, local fairway, and international fairway. These categories were treated as dichotomous variables in the model based on their presence. Since local fairways and confined water were highly correlated, only the confined water variable was included in the model. The port terminal berth areas and the low depth waters with scattered land obstacles were defined as confined waters. The fairways inside port waters were termed as local fairways, whereas those outside port waters were the international fairways.
Geometric characteristics of anchorages included the controlling water depth of navigation, presence of pilot boarding/disembarkation areas and the ratio of area to perimeter of anchorage. Pilot boarding/disembarkation areas were defined as the waters used by pilots to board or disembark an ocean-going vessel. The area-perimeter ratio was preliminarily considered to examine if there were any effects of the anchorage shape on collision potential, but it was omitted due to multi-collinearity. In addition, the variable representing presence of pilot boarding/disembarkation area was omitted from the analysis.
Characteristics of navigational aids (e.g., navigational buoys/lights) were represented by cardinal marks, isolated danger marks and safe water marks, as specified in the IALA Maritime Buoyage System (IALA, 1980). A cardinal mark indicates the safe side of the mark which shall be passed by vessels, whereas an isolated danger mark is used to indicate dangers (e.g., a small low-depth area which is surrounded by navigable waters). The safe water mark variable was omitted due to multi-collinearity.
Traffic characteristics included the average density of dynamic ships per square nautical mile, the average density of stationary ships per square nautical mile and the mean operating speed in an anchorage. A binary variable indicating day and night periods was considered to represent the navigational characteristics at these time periods.
4. ANALYSIS RESULTS
4.1. Measured Collision Potentials in anchorages
Collision potentials were measured by classifying vessels into four groups (based on vessel sizes): category 1 had gross tonnage (GT) between 300 and 12,000; category 2 had GT between 12,001 and 20,000; category 3 had GT between 20,001 and 75,000; and category 4 had GT more than 75,000. For each of these categories, the threshold values for separating serious conflicts from non-serious ones were adopted from Debnath and Chin (Reference Debnath and Chin2010).
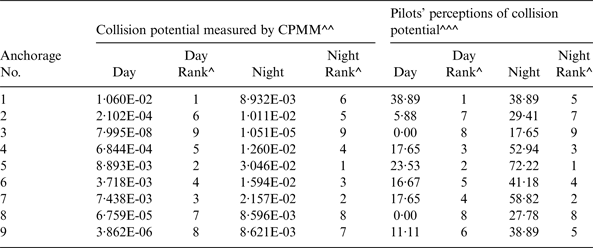
The measured collision potentials (i.e., probability of a serious conflict per encounter) for the anchorages studied are presented in Table 2. The probability values range from 8 in 100,000,000 to 1 in 100 during the day hours, and 1 in 100,000 to 3 in 100 during the night hours. The finding that the collision potentials are higher during the night hours than the day hours is consistent with findings obtained in earlier studies (e.g., Chin and Debnath, Reference Chin and Debnath2009; Debnath et al., Reference Debnath, Chin and Haque2011).
Table 2. Collision potentials measured by CPMM and perceived by harbour pilots.

^ Values ranked in descending order, ^^ Represent the probability of a serious conflict per encounter; ^^^ % pilots gave a rating of 3 or 4 on a scale of 0 to 4 (0: very unlikely, 1: Unlikely, 2: Moderate chance, 3: Likely, and 4: Very likely)
To validate the CPMM, the measured collision potentials of the anchorages were compared with those perceived by harbour pilots for the same anchorages. Existing research (Debnath and Chin, Reference Debnath and Chin2009a) showed that harbour pilots have a reasonably good understanding of the actual probabilities of collision in port waters. The perceived values were obtained from Debnath and Chin (Reference Debnath and Chin2009a) in which a detailed description of the perception survey can be found. In the survey, pilots were asked to rate the collision potentials of the anchorages shown in Figure 1. A five point scale representing the likelihood of a serious conflict in an anchorage (0: Very unlikely, 1: Unlikely, 2: Moderate chance, 3: Likely, and 4: Very likely) was used to collect the perceived ratings. From a pilot testing of the survey among several experienced pilots, it was decided to use the term ‘close quarter situation’, instead of ‘serious conflict’ in the survey as pilots are more familiar with the former term and both terms essentially carry a similar meaning. Pilots were asked to provide the ratings in each anchorage for an average pilotage job with an average vessel size that they generally operate (it is to be noted that Singapore port pilots generally operate vessels of one of the four size categories outlined in the previous paragraph, based on their experience and rank). The ratings were obtained separately for day and night periods. The survey, participation in which was voluntary and responses in which were anonymous, was sent to 160 harbour pilots of the Port of Singapore. A total of 70 completed survey forms (44% response rate) were received. The age of respondents ranged from 28 to 61 years with a mean and standard deviation of 43·0 years and 9·8 years respectively. The respondents had an average 11·3 years' experience as harbour pilots with a standard deviation of 10·9 years.
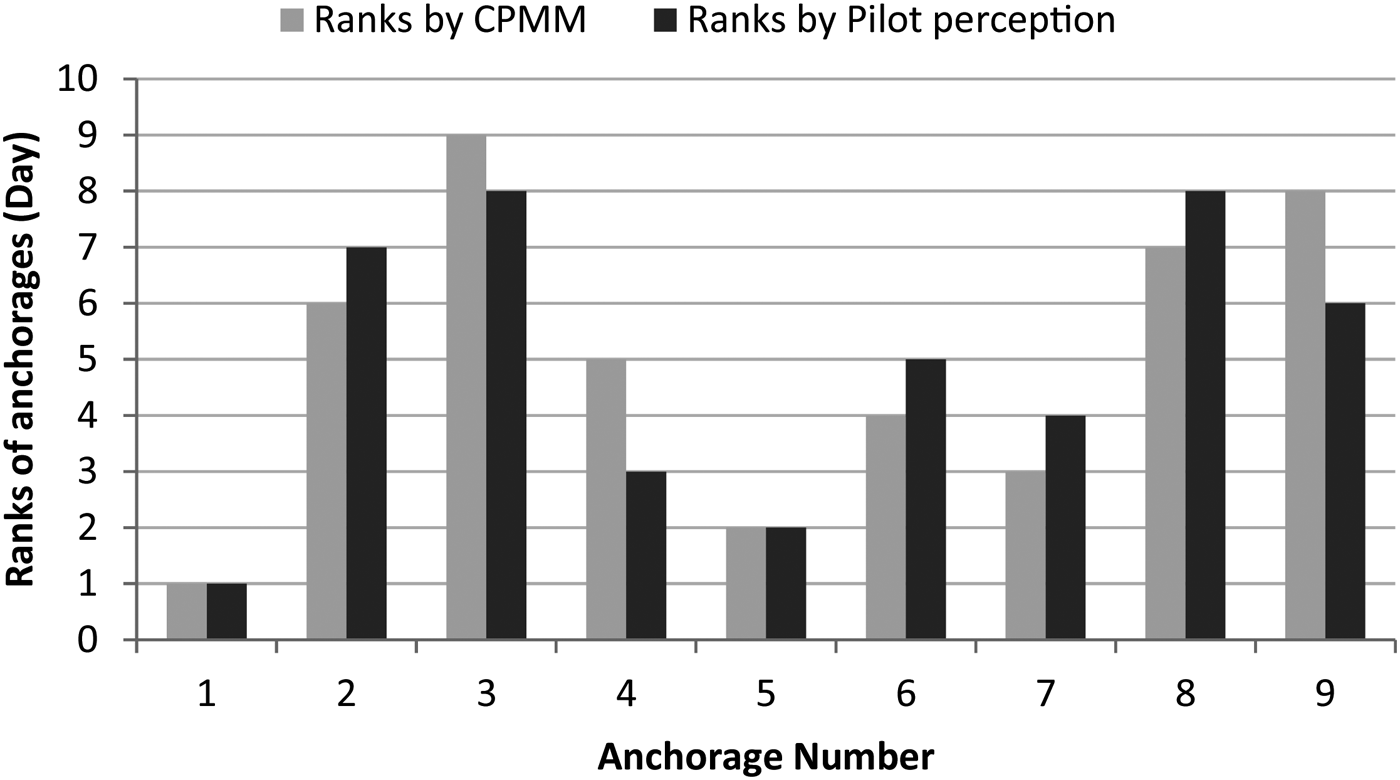
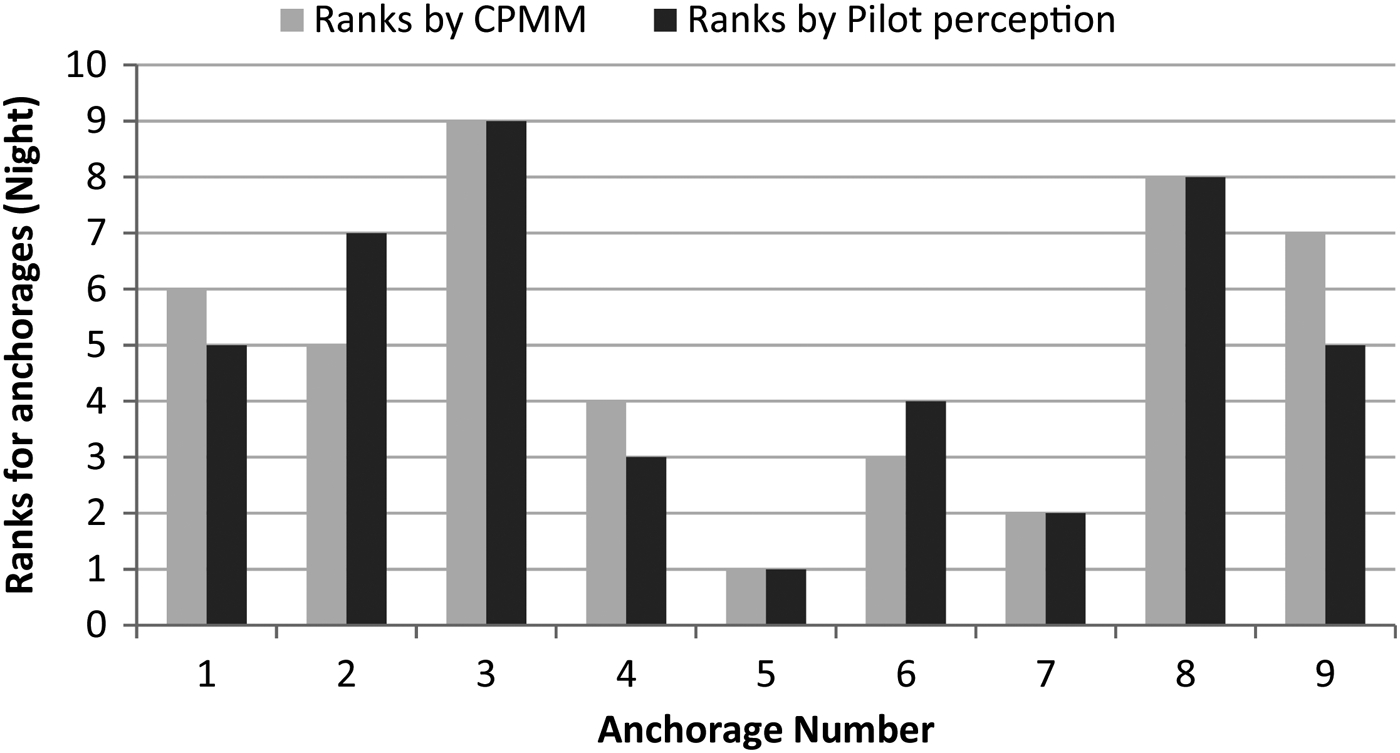
The anchorages are ranked in descending order of collision potentials for both the measured (by using the values obtained from the CPMM) and the perceived values (by computing the percentage of pilots giving a score of 3 or 4 on the five point scale). Comparison of the rankings for the day and night periods (presented in Figure 2 and Figure 3 respectively) indicate that the rankings of the anchorages according to the collision potentials measured by the CPMM match the rankings by the pilot perceptions reasonably well.

Figure 2. Comparison of the anchorage rankings for Day period.

Figure 3. Comparison of the anchorage rankings for Night period.
4.2. Regression Model Results
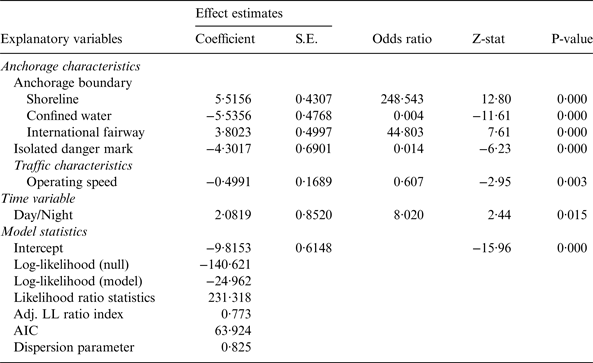
The parameters of the BLM were derived using the maximum likelihood estimation method. The potential correlations among observations within an anchorage were modelled using a modified sandwich variance matrix approach (see Debnath (Reference Debnath2009) for a detailed description of this approach). Starting with a saturated model that included all of the explanatory variables, a backward elimination procedure was employed to obtain the most parsimonious model by minimising the value of Akaike Information Criteria (AIC). The insignificant variables were omitted one after another starting with the most insignificant one. Estimates of the BLM along with their fitness statistics are presented in Table 3.
Table 3. Regression estimates of the RPM.

The most parsimonious BLM had an AIC value of 63·9 and a dispersion statistic of 0·83 (so adjustments to standard errors are not required). The Likelihood Ratio statistic of the model was 231·3, which is well above the critical value at 99% confidence level, implying that the model has a reasonably good fit. The Adjusted Log-likelihood Ratio Index (=0·77) also indicates that the model has sufficient explanatory and predictive power.
Turning to specific estimation results, the collision potential is significantly associated with presence of shoreline at the anchorage boundary (beta = 5·52, p < 0·001). Anchorages attached to the shoreline have 247 times higher odds of a serious conflict. Vessels have restricted access to this type of anchorage due to the presence of a shoreline at a boundary of these anchorages. Typically, vessels anchored near the shoreline need to navigate through the other anchored vessels in order to move out of the anchorage. Such movements generate more interactions (and possibly more conflicts) between vessels, resulting in higher probabilities of collision.
Anchorages bounded by confined waters have lower collision potentials (beta = −5·54, p < 0·001) with 250 times higher odds of non-serious conflicts. Confined water characterises low density and slow speed vessel movements in the berth areas, and only small vessels (e.g., pilot boats, speed boats) operate in these low depth waters. Collectively, these factors might reduce the collision potentials in anchorages bounded by confined waters.
The probability of serious conflicts significantly increases if an international fairway is present at the anchorage boundary (beta = 3·80, p < 0·001). Pilot boarding/disembarkation areas are usually located near the international fairways. These areas are used by pilots to go on board the vessels calling to a port or to disembark the vessels intending to leave the port. The boarding and disembarkation process is a safety critical event in navigation (SOLAS, 1974) and it often requires vessels to reduce speeds to make the process safer. Such reduction in speed could impede through-traffic movements in international fairways and, possibly, result in a greater number of conflicts because of the variation in speeds among successive vessels. In addition, interactions of pilot boats with the existing traffic may pose an additional likelihood of collision. Results showed that the odds of a serious conflict are 44 times higher if an international fairway is present at an anchorage boundary.
The number of isolated danger marks in anchorages have significant negative association with collision potentials in anchorages (beta = −4·30, p < 0·001). An isolated danger mark decreases the odds of a serious conflict by 98·6%. However, other research found that presence of an isolated danger mark increases the odds of serious conflicts in fairways (Debnath et al., Reference Debnath, Chin and Haque2011). The difference in the effects of isolated danger marks in fairways and anchorages could be observed due to the fact that operating speed is generally higher in fairways than in anchorages. At high speeds, it is necessary to take collision avoidance actions at an early stage. Failing to do so may increase the probability of collision. On the other hand, vessels operate at lower speeds in anchorages, thus it is possible to plan collision avoidance actions early.
Operating speed showed significant negative association with collision potentials in anchorages. An increase of 1 knot reduced the odds of a serious conflict by 39·3% (beta = −0·50, p = 0·003). This negative association might have been observed for a couple of reasons. Pilots might navigate at lower speeds when they foresee a difficult navigational situation ahead, arising from high density of anchored ships (i.e., less navigation room available than in a low density condition) or presence of other moving vessels nearby. The track-keeping ability of vessels, which is reduced at lower speeds, might also contribute to this negative association.
Pilots might navigate at higher speeds when the density of anchored ships is low (i.e., there is more navigation room and possibly less likelihood of collision) and vice versa. The track-keeping ability of vessels, which is reduced at lower speeds, might also contribute to this negative association.
The collision potentials were found to be higher during the night hours (beta = 2·08, p = 0·015) with 7·0 times higher odds of a serious conflict than during the day hours. This finding is consistent with those of other studies (Chin and Debnath, Reference Chin and Debnath2009; Debnath et al., Reference Debnath, Chin and Haque2011; Weng et al., Reference Weng, Meng and Qu2012). Arguably, the speeds and distances between vessels and even any moderate changes in course can be more readily judged during day than during night. At night, pilots need to rely on navigational aids (e.g., radar, navigational lights), which makes the risk perception and mitigation process more difficult than in the daytime. Effectiveness of navigational lights can also be reduced at night due to bright background lights on shore and from nearby islands (Akten, Reference Akten2004; Liu et al., Reference Liu, Liang, Su and Chu2006). A number of studies (Chin and Debnath, Reference Chin and Debnath2009; Debnath and Chin, Reference Debnath and Chin2009a; Debnath and Chin, Reference Debnath and Chin2009b) have also reported that pilots perceive higher collision risks at night.
5. CONCLUSIONS
Significant research efforts have been devoted to examining the safety issues related to collisions in port fairways and channels, but little attention has been given to understanding the safety issues at port anchorages. This paper aimed to fill this important gap in the literature by measuring collision potentials in anchorages and establishing relationships between the collision potentials and the various geometric, traffic, and regulatory control characteristics of anchorages.
A collision potential measurement model was developed by using the principles of the NTCT. This model provided a quantitative estimate of collision potentials in anchorages by analysing surrogate indicators of collision events (i.e., traffic conflicts). Collision potentials were expressed in terms of the probability of a serious conflict (an encounter which may lead to a collision event if appropriate evasive actions are not taken urgently) per vessel encounter (an interaction event between two vessels when one is within the ship domain of the others). The probabilities of serious conflicts were later modelled in a BLM framework to derive a prediction model. This model estimated the relationships between the probabilities of serious conflicts and the geometric, traffic, and regulatory control characteristics of anchorages.
Both the measurement and prediction models were illustrated for the anchorages in Singapore port waters. Results showed that the estimated collision potentials match those perceived by harbour pilots reasonably well thus providing evidence for the validity of the measurement model. Estimation results of the BLM showed that the collision potentials are higher in anchorages attached to shoreline and international fairways. On the other hand, the anchorages bounded by confined water had lower collision potentials. Similarly, lower collision potentials were observed in anchorages with lower operating speeds and higher numbers of isolated danger marks. Overall, the collision potentials in night hours were higher than those in day hours.
Future research should focus on 1) improving the CPMM by incorporating information related to vessel command (alertness or competence) into the information related to vessel movement trajectories, 2) expanding the CPPM by including more explanatory variables related to the geometric and traffic characteristics of the anchorages (e.g., the number of passing traffic on the fairways adjacent to the anchorages, types of vessels involved), and 3) extending the analyses of collision potentials in the anchorages by considering the different types of vessel interactions (e.g., interactions among anchored-anchored, anchored-underway, and underway-underway vessels).