1. Introduction
The availability of massive genetic marker information provides new opportunities for understanding quantitative variation, locating genes, molecular classification of disease status, designing genotype-specific regimes (e.g. diets or therapies) or for enhancing the accuracy of prediction of genetic merit in plant and animal breeding. A nice example of novel insight is provided by Visscher et al. (Reference Visscher, Medland, Ferreira, Morley, Zhu, Cornes, Montgomery and Martin2006) and Visscher et al. (Reference Visscher, Macgregor, Benyamin, Zhu, Gordon, Medland, Hill, Hottenga, Willemsen, Boomsma, Liu, Deng, Montgomery and Martin2007), who studied the genetics of height in humans. The authors infer genetic variation from information arising within families only, exploiting the variation in identity-by-descent shared between relatives, uncovered by marker information. They find that their data are consistent with a uniform spread of trait loci throughout the genome whose effects act additively on height. In animal and plant breeding several selection programmes are now genotyping elite individuals and genetic evaluations based on SNPs are becoming routine (González-Recio et al., Reference Gonzalez-Recio, Gianola, Long, Weigel, Rosa and Avendaño2008; Hayes et al., Reference Hayes, Bowman, Chamberlain and Goddard2009; VanRaden et al., Reference VanRaden, Van Tassell, Wiggans, Sonstegaard, Schnabel, Taylor and Schenkel2009; Hayes et al., Reference Hayes, Bowman, Chamberlain and Goddard2009). Considerable research efforts are currently devoted to the development of methods that incorporate massive marker information, and a large variety of models and approaches are becoming available.
The use of massive marker information in a linear regression model to predict genetic values for quantitative traits was first proposed by Meuwissen et al. (Reference Meuwissen, Hayes and Goddard2001). This model and others discussed in the literature postulate that quantitative trait loci (QTL) affect the mean of the quantitative trait, and assume homogeneity of residual variation. Sorensen (Reference Sorensen2009) suggests an extension to investigate whether genomic regions also have an effect on the environmental variance. Support for genetic regulation of the environmental variance has been reported for a number of traits in tomato (Weller et al., Reference Weller, Seller and Brody1988), litter size in sheep (San Cristobal-Gaudy et al., Reference San Cristobal-Gaudy, Bodin, Elsen and Chevalet2001), litter size in pigs (Sorensen & Waagepetersen, Reference Sorensen and Waagepetersen2003), adult weight in snails (Ros et al., Reference Ros, Sorensen, Waagepetersen, Dupont-Nivet, SanCristobal, Bonnet and Mallard2004), body weight in poultry (Rowe et al., Reference Rowe, White, Avendano and Hill2006; Wolc et al., Reference Wolc, White, Avendano and Hill2009; Mulder et al., Reference Mulder, Hill, Vereijken and Veerkamp2009), slaughter weight in pigs (Ibáñez et al., Reference Ibáñez, Varona, Sorensen and Noguera2007), litter size and weight traits in mice (Gutierrez et al., Reference Gutierrez, Nieto, Piqueras, Ibáñez and Salgado2006; Ibáñez et al., Reference Ibáñez, Moreno, Nieto, Piqueras, Salgado and Gutierrez2008a), litter size in rabbits (Ibáñez et al., Reference Ibáñez, Sorensen, Waagepetersen and Blasco2008b), bristle counts in Drosophila (Whitlock & Fowler, Reference Whitlock and Fowler1999; Mackay & Lyman, Reference Mackay and Lyman2005), a number of traits in maize (Ordas et al., Reference Ordas, Malvar and Hill2008) and levels of gene expression in yeast (Ansel et al., Reference Ansel, Bottin, Rodriguez-Beltran, Damon, Nagarajan, Fehrmann, François and Yvert2008). With the exception of the first and last two references, inferences were based on models for the residual variance where marker information was not included. Ordas et al. (Reference Ordas, Malvar and Hill2008) analysed a number of maize recombinant inbred lines and incorporated information on 85 genetic markers. The design made it possible to use a simple analysis, including a fixed effect of genotype in the least-squares linear model for residual variances. Ansel et al. (Reference Ansel, Bottin, Rodriguez-Beltran, Damon, Nagarajan, Fehrmann, François and Yvert2008) provide convincing evidence for heterogeneity of gene expression in isogenic yeast cells of different genotypes and identify three QTLs involved in the control of heterogeneity.
The purpose of this work is to incorporate marker information to detect genomic regions that have effects on the residual variance. The standard genomic model operating on the mean of a quantitative trait is extended to accommodate marker covariates on the log-environmental variance, and two models are proposed. The first one assumes that marker effects at the level of the mean and variance are a priori bivariate normally distributed, with common mean and covariance matrix. The second model is based on stochastic search variable selection (George & McCulloch, Reference George and McCulloch1993). It assumes that marker effects at the level of the mean and variance are independent a priori and that their distributions are two-component normal mixtures. The models are implemented using Markov chain Monte Carlo (McMC) and their ability to detect QTL is studied using simulated data. Subsequently the models are fitted to back fat thickness data in pigs.
This paper is organized as follows: Section 2, introduces the genomic models and describes the McMC algorithm. Section 3 describes the types of data simulated and the inferences that are possible from the various models. Section 4 contains results of the application to back fat data. Section 5 discusses issues related to the relative sizes of experiment to detect marker effects at the level of mean and variance and proposes an extension of the McMC algorithm.
2. Methods
Four models are studied that differ in the structure of the residual variance of the likelihood and in the prior distributions of marker effects at the level of the mean and variance. Two classes of prior distributions of marker effects are considered, and the residual variance is assumed to be either homogeneous or genetically heterogeneous. The first two models assume that marker effects are independent and identically normally distributed. Model GHOM includes marker effects at the level of the mean only with identical distribution and homogeneous residual variance. The heterogeneous variance model GHET assumes marker effects on the mean and on the log-variance of the trait, and for marker j, the pair of marker effects (affecting mean and variance) is bivariate normally distributed. The third and fourth models assume that marker effects originate from identical two-component mixture distributions. In the model labelled GHOMMIX, marker effects operate at the level of the mean only and the variance is homogeneous. The final heterogeneous variance model is GHETMIX, where the pair of marker effects on mean and variance for marker j are independently distributed, and each originates from a two-component mixture.
(i) Likelihood
The sampling distribution of the data is Gaussian of the form

where y is the data vector of length n, 1 is a vector of ones, the scalar μ is the mean, a is a vector of marker effects on the mean and σ2 i,M is the environmental variance for the ith observation under model M. The matrix X is an n×N matrix where Xij is an observable indicator for the jth marker locus of the ith individual, coded as −1 for genotype 11, 0 for genotype 12 and 1 for genotype 22, and N is the number of marker loci. The conditional likelihood is proportional to (1). Here and elsewhere we use N(·,·) to denote both a normal distribution and its density function.
In the genomic model with homogeneous variance (GHOM and GHOMMIX), σi,12=exp (μ*) (Meuwissen et al., Reference Meuwissen, Hayes and Goddard2001). Genetic heterogeneity of environmental variance (in models GHET and GHETMIX) is incorporated by assuming that
where x′ i is the ith row of X, and a* is the column vector with N marker effects on the variance (Sorensen, Reference Sorensen2009).
(ii) Prior specifications
The mean μ and the environmental variance when a*=0, exp (μ*), are assigned improper uniform distributions. Depending on the model, two possible distributions are assigned to vector a or vectors (a, a*). The first one is a common Gaussian distribution for all marker effects. A mechanistic justification for this distribution is to assume that markers capture the effects of loci with which they are in disequilibrium. These effects are of similar magnitude across loci and therefore can be approximated by a common Gaussian model. The second distribution is a mixture, such that a small proportion of loci originate from a normal distribution with relatively large variance, allowing a broad range of marker effects, that are captured by the markers. The rest of the loci have normally distributed effects with zero mean and very small variance. These loci can be interpreted as having no detectable effects on the trait.
(a) No mixture models
In models GHOM and GHET, marker effects are assumed to be independent realizations from the same normal process. In the GHOM model, the vector of marker effects a is assumed to have the normal prior distribution
where I is the identity matrix and σ2
a
is the variance of marker effects representing their prior uncertainty. This variance is assigned a scaled inverse chi-square distribution with degree of freedom ν and scale parameter ![]() . This prior specification was used by Legarra et al. (Reference Legarra, Robert-Granie, Manfredi and Elsen2008). The method known as BayesA (Meuwissen et al., Reference Meuwissen, Hayes and Goddard2001) instead assigns marker-specific variances, which are assumed to be realizations from a common scaled inverted chi-square distribution with known hyperparameters. This generates a problem of identifiability as noted by Gianola et al. (Reference Gianola, de los Campos, Hill, Manfredi and Fernando2009).
. This prior specification was used by Legarra et al. (Reference Legarra, Robert-Granie, Manfredi and Elsen2008). The method known as BayesA (Meuwissen et al., Reference Meuwissen, Hayes and Goddard2001) instead assigns marker-specific variances, which are assumed to be realizations from a common scaled inverted chi-square distribution with known hyperparameters. This generates a problem of identifiability as noted by Gianola et al. (Reference Gianola, de los Campos, Hill, Manfredi and Fernando2009).
In the GHET model, marker effects (a, a*) also have a common prior distribution of the form
where G is the 2×2 variance–covariance matrix
Thus, the pair of scalars (aj,aj
*) for the jth marker, is bivariate normally distributed. In eqn (4), ρ is the correlation between marker effects at the level of mean and variance, and σ
a
2 and ![]() are variances for marker effects a and a*, respectively. The parameter ρ is assigned a uniform prior bounded in (−1,1), and σ
a
2 and
are variances for marker effects a and a*, respectively. The parameter ρ is assigned a uniform prior bounded in (−1,1), and σ
a
2 and ![]() are assigned scaled inverted chi-square distributions with degrees of freedom ν and scale parameters
are assigned scaled inverted chi-square distributions with degrees of freedom ν and scale parameters ![]() and
and ![]() , respectively.
, respectively.
(b) Mixture models
In model GHOMMIX, the two-component normal mixture prior for marker effect aj is
where p is the probability that the effect is a realization from the normal component with variance c 2τ2, and the complement, (1−p) is the probability that it originates from the normal component with variance τ2. The term τ2 is chosen to be small, which results in aj ′s very close to zero. The distribution with larger variance c 2τ2, allows for the effects to depart markedly from the mean of zero and this is interpreted as a signal of the existence of a QTL in the proximity of the marker. The larger variance is obtained by setting c large.
The variance of the marker effect is
As in George & McCulloah (Reference George and McCulloch1993), the mixture prior is implemented augmenting with a set of independent binary indicator variables δ′=(δ1, …, δN), such that when δ j =1, aj has density N(0, c 2τ2), and when δ j =0, aj has density N(0, τ2). Then

and
Since the δj′s are independent with the same distribution,
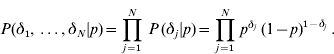
The joint prior distribution of all marker effects a and binary indicator variables δ is then
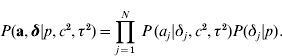
In the implementations that follow, the parameters c 2, τ2 and the probability p are treated as constants and must be tuned by the user.
The GHOMMIX model is in the same spirit as the so-called BayesB method (Meuwissen et al., Reference Meuwissen, Hayes and Goddard2001). However, in BayesB each marker is assigned a specific variance which as discussed in Gianola et al. (Reference Gianola, de los Campos, Hill, Manfredi and Fernando2009) leads to the same identifiability problem as BayesA. Further, in BayesB the mixture structure is specified at the level of the marker variances rather than at the level of the marker effects as in GHOMMIX.
The GHETMIX model involves also marker effects at the level of the environmental variance. It is assumed that marker effects at the level of mean aj and variance aj * are independent a priori. At the level of the mean, marker effects are as in eqn (7), and at the level of the residual variance, the normal mixture distribution of marker effects a j* is implemented augmenting with a set of independent binary indicator variables δ*′=(δ1*, …,δN*), such that when δ j *=1, aj * has density N (0,c*2τ*2), and when δ j *=0, aj * has density N (0,τ*2). Then
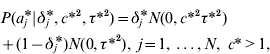
with
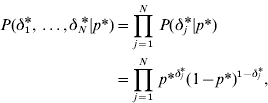
where
and p* is the probability that the marker effects at the level of variance is a realization from the normal component with variance c*2τ*2. On the basis of the above prior specifications, the joint prior distribution for (aj,aj *) conditional on (δ j ,δ j *) in model GHETMIX can be written as

where
In this GHETMIX model, the parameters c 2, c*2, τ2, τ*2 and the probabilities p and p* are treated as constants and must be tuned by the user. A way of choosing c and τ2 is described in the next subsection.
The parameterization in terms of the indicator functions δ j and δ j * provides a simple way of studying the ability of the GHOMMIX and GHETMIX models to detect QTL signals. For each marker, the posterior probabilities P(δ j =1|y) and P(δ j *=1|y) provide evidence for the presence of a QTL in the proximity of marker j. In section 3, we provide evidence for the presence of QTL via the Bayes factor, computed as
Monte Carlo estimates of these posterior probabilities are obtained using the draws from the Markov chain.
(iii) Choice of user-specified tuning parameters and an overview of effect on inferences
In the GHOMMIX model, the parameters c 2, τ2 and the probability p are treated as constants and must be tuned by the user. The following rule has been followed to choose values for these parameters. First, p is set to 0·10, so that 10% of the markers are assumed to have a detectable effect on the mean of the trait, a priori. A rough candidate value for τ2 is derived as follows. First, an analysis based on the classical infinitesimal model with homogeneous residual variance (using pedigree information only) yields an estimate of the additive genetic variance for the trait, σ2 u . Let ν j be the frequency of marker allele j, and assume that markers account for the component of genetic variation equal to 2∑ j ν j (1−ν j )aj 2. Then as shown by Habier et al. (Reference Habier, Fernando and Dekkers2007) and Gianola et al. (Reference Gianola, de los Campos, Hill, Manfredi and Fernando2009) a value for Var(aj ) can be obtained from
The value of τ2 is then set to two orders of magnitude smaller than Var(aj ). The parameter c 2 is finally obtained from eqn (6). The idea behind this way of choosing τ2 and c 2τ2 is to obtain components of the mixture that have the ability to discriminate between markers whose effects on the trait are barely detectable, from those with clearer effects.
The specification of c*2, τ*2 and p* on the GHETMIX model involves setting p*=0·10 and fitting first the infinitesimal genetically heterogeneous variance model described in Sorensen & Waagepetersen (Reference Sorensen and Waagepetersen2003) to obtain an estimate of ![]() , the additive genetic variance at the level of the log-variance. The remaining parameters τ*2, c*2 are then obtained as in the GHOMMIX model. In the simulation study below we used values of c and c* approximately equal to 45.
, the additive genetic variance at the level of the log-variance. The remaining parameters τ*2, c*2 are then obtained as in the GHOMMIX model. In the simulation study below we used values of c and c* approximately equal to 45.
A little intuition for how inferences may be affected by the choice of c can be obtained as follows. The model specifies that when δ
i
=1, the SNP effect is a realization from N(0,τ2) and when δ
i
=1, from N(0, c 2τ2). It is readily seen that the ratio of the heights of N(0, τ2) and N(0, c 2τ2) at aj
=0 is equal to c (George & McCulloch, Reference George and McCulloch1993). That is, c can be interpreted as the prior odds of allocating the SNP to the distribution N(0, τ2) when aj
is very close to zero. Insight about posterior inferences can be gained by assuming a simple scenario, whereby the model for the data when δ
i
=0 is of the form yij
|ai
,σ2~N(ai
, σ2) and ai
|τ2~N(0, τ2), i=1, …, n, j=1, …, ni
, where ni
is the number of records with genotype i whose effect is ai
. On the other hand, when δ
i
=1, ai|c 2τ2~N(0,c 2τ2). Standard calculations show that the posterior distribution [ai|y,δi
=0] is ![]() , and the posterior distribution [ai|y,δi
=1] is
, and the posterior distribution [ai|y,δi
=1] is ![]() , where
, where ![]() is BLUP of ai
. The Bayes factor for testing the null hypothesis H 0 of ai
=0 against the alternative H 1 that ai≠0, computed using the Savage–Dickey ratio (Verdinelli & Wasserman, Reference Verdinelli and Wasserman1995), given δ
i
=1, is
is BLUP of ai
. The Bayes factor for testing the null hypothesis H 0 of ai
=0 against the alternative H 1 that ai≠0, computed using the Savage–Dickey ratio (Verdinelli & Wasserman, Reference Verdinelli and Wasserman1995), given δ
i
=1, is

where both N(0, c 2τ2) and ![]() are evaluated at ai
=0. For example, when
are evaluated at ai
=0. For example, when ![]() , τ2=0·00005, σ2=4, for values of c=(40;400), B 01 takes values (0·051; 0·072), (1·08×10−3; 1·79×10−3), (5·4×10−6; 9·1×10−6), when ni
=100, 500, 1000, respectively. The evidence against the null hypothesis increases with the amount of data ni
, and the tuning parameter c has a modest effect on this inference.
, τ2=0·00005, σ2=4, for values of c=(40;400), B 01 takes values (0·051; 0·072), (1·08×10−3; 1·79×10−3), (5·4×10−6; 9·1×10−6), when ni
=100, 500, 1000, respectively. The evidence against the null hypothesis increases with the amount of data ni
, and the tuning parameter c has a modest effect on this inference.
(iv) McMC algorithm
The models are implemented using McMC algorithms, where the components in each model are updated sequentially. In general, the McMC algorithm for each model is based on a combination of Gibbs updates, updates based on random walk proposals and updates based on Langevin–Hastings proposals. In addition, a reparameterization described in Sorensen & Waagepetersen (Reference Sorensen and Waagepetersen2003) and Waagepetersen et al. (Reference Waagepetersen, Ibafiez and Sorensen2008) is made to improve the mixing of the algorithms. The vector (a, a*) is transformed in its prior distribution to an independently distributed vector (γ, γ*), with the intention of reducing the posterior correlation. In the GHET model, using the factorization G=LGL′
G
, where ![]() is the lower triangular Cholesky factor of the variance–covariance matrix G, (aj,aj
*)′ is reparameterized into LG
(γj,γj
*)′, j=1, …,N, leading to
is the lower triangular Cholesky factor of the variance–covariance matrix G, (aj,aj
*)′ is reparameterized into LG
(γj,γj
*)′, j=1, …,N, leading to
the density of a multivariate normal distribution with mean vector 0 and variance matrix equal to the identity matrix.
In model GHETMIX, (aj, aj
*)′ is reparameterized into ![]() , where (γj,γj*) has the a priori density as in eqn (8).
, where (γj,γj*) has the a priori density as in eqn (8).
In summary, the McMC algorithms for the four models are as follows:
1. For model GHET, μ, exp (μ*), (γ,γ*) and
 are updated in turn using Gibbs updates for μ and exp(μ*), Metropolis–Hastings updates with Langevin–Hastings proposals for (γ, γ*), and random walk proposals for σ
a
2,
are updated in turn using Gibbs updates for μ and exp(μ*), Metropolis–Hastings updates with Langevin–Hastings proposals for (γ, γ*), and random walk proposals for σ
a
2,  (on the log scale) and ρ.
(on the log scale) and ρ.2. The same algorithm is used for model GHOM, with γ*,
 and ρ omitted from the algorithm.
and ρ omitted from the algorithm.3. For model GHETMIX, μ, exp (μ*), δ j and δ j * are updated using Gibbs steps, with fully conditional posterior distributions parameterized in terms of (a, a*). These are transformed into (γ, γ*), which is updated using a Langevin–Hastings proposal.
4. Model GHOMMIX is based on the same algorithm as for model GHETMIX with γ* and δ* omitted from the algorithm.
The McMC algorithms run for 1 800 000 cycles after discarding the first 400 000 cycles as burn-in period. The chains were thinned (saved one iteration every 140 cycles), so that the total number of samples kept was 10 000 for all models. Convergence was checked informally looking at traceplots of chosen parameters (data not shown). The algorithms showed good mixing properties. The smallest effective chain size (Sorensen et al., Reference Sorensen, Andersen, Gianola and Korsgaard1995) corresponding to ![]() for the GHET model was equal to 1080. This resulted in a 95% Monte Carlo interval equal to 1·4% relative to the posterior mean.
for the GHET model was equal to 1080. This resulted in a 95% Monte Carlo interval equal to 1·4% relative to the posterior mean.
(v) Model comparison
The models were evaluated with three criteria, using both simulated data (where the true state of nature is known) and real data. Firstly, interest focused on the ability of GHETMIX and GHET models to detect QTL signals at the level of the mean and variance. Secondly, a measure of the quality of the global fit of the models is reported. It is relevant to study whether this can be used to discriminate among the models’ ability to capture the true state of nature. The third criterion is the predictive ability of the models. Additive genetic values were predicted and compared with the true ones using simulated data and cross-validation was used with the real data.
The quality of the global fit of the models was compared using the pseudo marginal probability of the data (Gelfand, Reference Gelfand, Gilks, Richardson and Spiegelhalter1996) that is defined and computed as follows. Consider data vector y′=(yi , y′−i), where yi is the ith datum, and y −i is the vector of data with the ith datum deleted. For a particular model M, the conditional predictive distribution is
and can be interpreted as the likelihood of each datum given the remainder of the data. The actual value of P(y i|y−i,M) is known as the conditional predictive ordinate (CPO) for the ith observation, where θ is the vector of model parameters. A Monte Carlo approximation to the CPO in eqn (9) for observation i is given by (Gelfand, Reference Gelfand, Gilks, Richardson and Spiegelhalter1996)
where K is the number of McMC draws and θ(k) is the kth draw from the posterior distribution of θ under model M.
For a given model, the log-pseudo-marginal probability of the data is ∑n i =1log(CPO i ), which is a surrogate for the Bayes factor (Geisser & Eddy, Reference Geisser and Eddy1979; Gelfand et al., Reference Gelfand, Dey, Chang, Bernardo, Berger, Dawid and Smith1992). A larger value of ∑n i =1log(CPO i ) indicates a better relative fit. The log-pseudo-marginal probability of the data is used to compare different genomic models.
3. Simulation study
The aim of the simulation study is to examine properties of the proposed methods in their ability to detect QTL signals and predicting breeding values. A third objective is to study whether the models are capable of capturing the true state of nature. This is done by fitting the four models to simulated data and computing the log-pseudo-marginal probability of the data under each model.
The data were simulated mimicking two scenarios. In scenario 1, a total of eight QTLs were placed in five chromosomes with length 100 cM each. Of these eight QTLs, four affected mean only, and four affected variance only. In both cases, three QTLs were assumed to have relatively substantial effects and one had a relatively little effect. In scenario 2, 80 QTLs were placed along the five chromosomes. Of these 80 QTLs, 30 had the effects only on the mean, 30 only on the variance and 20 were pleiotropic with the effects on both. In the two scenarios 4779 biallelic SNP markers evenly distributed in five chromosomes at a distance of approximately 0·1 cM between adjacent markers were available to detect the QTL.
The data were simulated as follows. Initially, a population size of 100 individuals was created, of which half were females and the other half males. Each of these individuals was allocated a genotype with 5000 biallelic SNP markers evenly placed in the five chromosomes. In addition, at this stage, 100 QTLs were randomly placed in the five chromosomes. Recombination between adjacent loci was generated using Haldane's mapping function (with no interference). A total of 50 generations of random mating were simulated. At generation 51, the population size was incremented to 100 males and 1000 females, and kept constant at a size of 1100 individuals for two extra generations. Each of the 100 males mated to 10 females. Thus, at generation 52, the pedigree consisted of full-sibs (one male and one female) and of half-sib families. A similar strategy was used to produce individuals of generation 53. The data for analysis belong to generations 51–53. At this final stage, the QTLs were allocated an effect and markers with a gene frequency smaller than 0·05 were discarded. A total of 4779 marker loci satisfied this criterion and were included in the final data set. Among these 3300 individuals of generations 51, 52 and 53, the average squared correlation of gene frequencies between adjacent pairs of marker loci (approximately 0·1 cM apart) was 0·20. The results of Calus et al. (Reference Calus, Meuwissen, de Roos and Veerkamp2008) and Meuwissen et al. (Reference Meuwissen, Hayes and Goddard2001) suggest that this level of linkage disequilibrium is sufficient to achieve high accuracies of prediction of genomic breeding values.
Genetic variation was generated as follows. QTL j was allocated an effect b j and its additive genetic variance at the level of the mean was computed as ![]() , where q j is the observed frequency of the favourable allele at QTL j. In scenario 1, the values of b j (in absolute values) range from 0·2 to 1·5 units, and in scenario 2 from 0·2 to 0·45 units. At the level of the variance, these figures are 0·3–1·5 for scenario 1, and 0·20–0·45 for scenario 2. The total additive genetic variance at the level of the mean, σb2, was defined as the sum of the contributions
, where q j is the observed frequency of the favourable allele at QTL j. In scenario 1, the values of b j (in absolute values) range from 0·2 to 1·5 units, and in scenario 2 from 0·2 to 0·45 units. At the level of the variance, these figures are 0·3–1·5 for scenario 1, and 0·20–0·45 for scenario 2. The total additive genetic variance at the level of the mean, σb2, was defined as the sum of the contributions ![]() from each QTL, ignoring the correlation structure due to linkage disequilibrium. The total additive genetic variance at the level of the environmental variance, σb*2, was generated in a similar manner, by summing contributions
from each QTL, ignoring the correlation structure due to linkage disequilibrium. The total additive genetic variance at the level of the environmental variance, σb*2, was generated in a similar manner, by summing contributions ![]() from each QTL.
from each QTL.
In the two simulated scenarios, the overall mean was μ=50 and the total additive genetic variances (ignoring the covariance due to linkage disequilibrium) at the level of the mean and variance (σb2 and σb*2) are equal to 1·98 and 1·85. The term exp (μ*) was set equal to 2·00, which resulted in a heritability equal to 0·28. The value of σb*2 used in these scenarios is rather large compared to the estimates reported in the literature (summarized in Mulder et al., Reference Mulder, Bijma and Hill2007). The implications for the probability of detecting effects on mean and variance are elaborated in the discussion.
The 2200 individuals from generations 51 and 52 are allocated a single phenotypic record, whereas the 1100 from generation 53 have only genotypic values, determined by the sum of the effects of the individual QTL.
(i) The detection of QTL
For simulated scenario 1, the ability of the GHETMIX model to detect signals is displayed at the top of Fig. 1. For the three QTLs of relatively large effect on the mean, in chromosomes 1, 3 and 4, the Monte Carlo estimates of the posterior probabilities P (δj|y,M) of the markers closest to these QTL are in the vicinity of 1. However, the model fails to detect the signal in chromosome 2 due to the QTL of small effect. The picture concerning detection at the level of the variance (top, right of Fig. 1) is very similar. The bottom of Fig. 1 shows posterior means of marker effects from the GHET model plotted against their position in the genome. There is overall agreement between the results from both models.

Fig. 1. Simulated scenario 1. Top: results from the GHETMIX model, with p=p*=0·1 and (τ2, c 2τ2, τ*2, c*2τ*2)= (0·5×10−5, 0·1×10−1, 0·5×10−5, 0·1×10−1). The true QTL effects (b and b*, black triangle pointing upwards) and posterior probabilities of marker indicators (blue solid circles) are plotted against marker locations along the genome with effects on mean (left) and on environmental variance (right). Bottom: similar results from the GHET model, with posterior means of marker effects a and a* in the Y-axis.
The mixture models have the attractive property that they readily provide Monte Carlo estimates of Bayes factors as evidence for the presence/absence for a QTL at each SNP via the ratios of posterior to prior odds of detection. For example, for the SNP on chromosome 1 affecting mean, the Bayes factor is (0·97/0·03)/(0·10/0·90)=291, which is decisive evidence for the presence of a QTL associated with the SNP (see Kass & Raftery (Reference Kass and Raftery1995), for guidelines for interpreting actual values). A posterior probability of 0·5 results in a Bayes factor equal to (0·5/0·5)/(0·10/0·90)=9, which is interpreted as substantial evidence for the presence of a QTL associated with the SNP.
The performance of GHETMIX model under simulated scenario 2 is shown in Fig. 2. The model can detect QTL successfully at the level of the mean. Indeed, for many of the markers close to the QTL, the posterior probabilities of the indicator variable is in the proximity of 0·5, and these are scattered along the genome, in agreement with the genetic model. Similar results hold at the level of the variance with several markers associated with posterior probabilities of the indicator variable around 0·5 and a few at higher values. Inferences from GHET model are shown at the bottom of Fig. 2. The signals are also scattered along the genome in agreement with the true genetic model, with a few markers showing larger effects than the rest. The pattern is similar as with the GHETMIX model. Arguably, the size of the estimates of SNP effects from the GHET model, as a source of evidence for the presence of regions affecting the trait, is not as clear to interpret as the posterior probabilities generated by the mixture models.

Fig. 2. Simulated scenario 2. Top: results from the GHETMIX model, with p=p*=0·1 and (τ2, c 2τ2, τ*2, c*2τ*2)=(0·5×10−5, 0·11×10−1, 0·5×10−5, 0·01). The true QTL effects (b and b*, black triangle pointing upwards) and posterior probabilities of marker indicators (blue solid circles) are plotted against marker locations along the genome with effects on mean (left) and on environmental variance (right). Bottom: similar results from the GHET model, with posterior means of marker effects a and a* in the Y–axis.
(ii) Model comparison
The results of the model comparison are shown in Table 1. The four models were fitted to the data simulated under scenarios 1 and 2, and the log-marginal probability of the data under each model is computed (third column of Table 1). In both scenarios, the ∑ilog (CPOi) were relatively larger under the models postulating QTL effects at the level of mean and variance (models GHET and GHETMIX), and the best overall fit is obtained with the GHETMIX model.
Table 1. The log-pseudo-marginal probability of the data and correlation (Corr(TBV, PGBV)) between true (TBV) and predicted genomic breeding value (PGBV), at the level of the mean and variance, obtained from the four models fitted to data simulated under scenarios 1 and 2. In both scenarios, p=0·1 and p*=0·1. In scenario 1, (τ2, c2τ2, τ*2, c*2τ*2)=(0·5×10−5, 0·1×10−1, 0·5×10−5, 0·1×10−1), and in scenario 2, (τ2, c2τ2, τ*2, c*2τ*2)=(0·5×10−5, 0·11×10−1, 0·5×10−5, 0·01)

(iii) Genomic prediction
The predictive ability of the four models is studied computing the correlation between the true breeding values and the predicted genomic breeding values. The predicted genomic breeding value at the level of the mean for the ith individual is
and a similar predicted genomic breeding value at the level of the variance (with obvious notation) is
where wi is the column vector of marker genotypes for the ith individual in generation 53, coded as −1 for genotype 11, 0 for genotype 12 and 1 for genotype 22. We distinguish the genotypic indicator matrix X of individuals belonging to generation 51 and 52 from W, associated with those of 53. The ![]() and
and ![]() are the vectors of posterior means of marker effects operating at the level of mean and variance among individuals belonging to generation 53, estimated from a given model using phenotypes belonging to generations 51 and 52.
are the vectors of posterior means of marker effects operating at the level of mean and variance among individuals belonging to generation 53, estimated from a given model using phenotypes belonging to generations 51 and 52.
Results are shown in the last two columns of Table 1. At the level of the mean, model GHETMIX produces the largest correlations for scenarios 1 and 2, and the difference in favour of model GHETMIX is relatively more visible in the first scenario. The GHOM model results in the smallest correlations in both scenarios.
At the level of the variance, the difference in favour of model GHETMIX relative to model GHET is also more pronounced in scenario 1.
The results from the genomic models can be placed in perspective by comparing with the correlations achievable using pedigree information only, ignoring marker information. An additive model with homogeneous environmental variance resulted in a correlation between true and predicted breeding values, at the level of the mean, equal to 0·516. The additive model with genetically structured environmental variance produced a value of 0·522, and at the level of the environmental variance, the correlation between true and predicted breeding values was 0·400. For this simulated data set, there is a clear difference in favour of the genomic models. The predictive performance of a model with both polygenic and marker effects was not included in this study. Calus & Veerkamp (Reference Calus and Veerkamp2007) show that very little is gained using such a model unless the average squared correlation coefficient between adjacent markers is lower than 0·10 for low heritability traits and lower than 0·14 for high heritability traits. On the other hand when the focus is detection of genomic regions rather than prediction, omission of a polygenic effect may affect inferences in at least two ways. Firstly, not accounting for the correlated error structure induced by the polygenes can lead to underestimation of uncertainty. Secondly, effects of the omitted polygenes may be captured by the SNPs leading to overestimation of their effects. These consequences are likely to be more pronounced at low SNP marker densities. This has not been investigated in the present work.
4. Real data analysis – back fat thickness in pigs
Results of a pilot study are reported using back fat thickness measurements taken on 960 Landrace boars from the Danish nucleus breeding herds. The objective is to illustrate the application of the methods developed rather than studying details of the genetic architecture of the trait.
(i) Data
SNP marker genotypes of 960 boars were obtained using a 6 K Illumina bead chip, from which 2011 SNPs had good quality and minor allele frequency larger than 5%. Each of the 960 boars has also a back fat record, which was corrected for weight prior to the analysis. The square root of back fat was used since in this scale the posterior distribution of the coefficient of skewness is symmetrical. The heritability based on a classical infinitesimal model was estimated to be 0·24.
A glance at the pedigree file constructed using two-generation data revealed that the genotyped offspring consisted of 225 full-sibs, 405 half-sibs, and the remaining individuals were unrelated. This pedigree information is not incorporated into the genomic models used in the present study. Similar data were used by Janss et al. (Reference Janss, Nielsen, Christensen, Bendixen, Sørensen and Lund2009).
(ii) The detection of QTL
Fig. 3 shows the results from fitting the GHETMIX (top) and GHET (bottom) models to back fat data. The top figure on the left is suggestive of the presence of genomic regions with effects on the mean. Five of these are associated with posterior probabilities of the indicator function larger than 0·45, and for one of these five, the probability is larger than 0·65. Results from fitting the GHET model lead to similar conclusions. Both models fail to produce signals suggesting detectable effects on the variance (right panels).
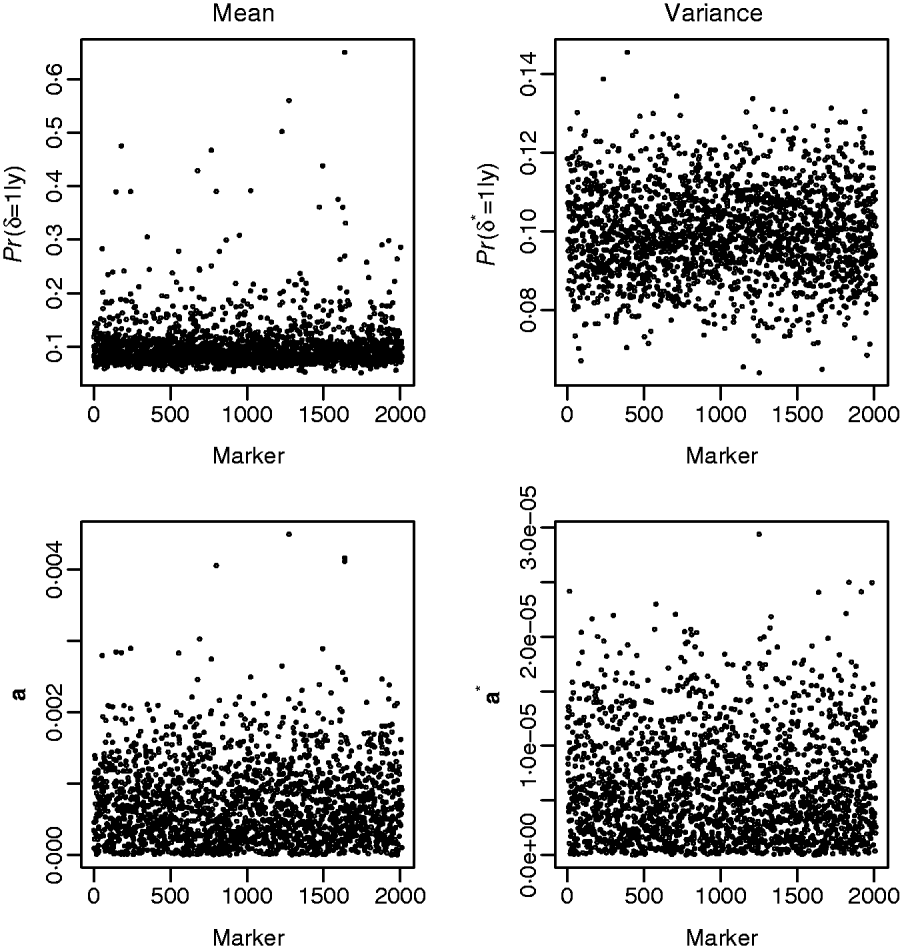
Fig. 3. Back fat data. Top: results from the GHETMIX model, with p=p*=0·1 and (τ2, c 2τ2, τ*2, c*2τ*2)=(0·5×10−7, 0·1×10−3, 0·5×10−9, 0·2×10−5). Posterior probabilities of the indicator function plotted against marker number for QTL effects on mean (left) and on environmental variance (right). Bottom: results from the GHET model, with posterior means of marker effects a affecting mean (left) and variance a* (right) in the Y–axis.
Another way of viewing the results is displayed in Fig. 4, that shows the distribution of Monte Carlo estimates of the posterior probabilities of the indicator function across the markers at the level of the mean (left), P (δj=1|y), and at the level of the variance, P (δj*=1|y), (right) obtained from model GHETMIX. The Monte Carlo estimate of the posterior probability associated with each marker, is obtained by summing the Monte Carlo draws of the marker's indicator function over the Monte Carlo samples, and dividing by the number of samples. The left figure indicates that most of the markers are associated with very small probabilities, essentially reproducing the prior probability (0·10), indicating absence of QTL in their proximity. However, the figure uncovers the five markers with relatively larger effects on the mean that are vaguely discernible at the larger end of the probability scale. The histogram on the right reflects what is to be expected if the data are uninformative about the marker indicator δ*, so that P (δj*=1|y)=P (δj*=1|p)=p. In this case, the value of 1 for the indicator function is randomly assigned to the markers with probability p. The histogram represents the sampling distribution of the Monte Carlo estimator of P (δj*=1|y), μj=1/K∑t=1KI (t) (δj=1|p), where I (t) (δj=1|p) is the value of the indicator function for marker j in round t, and K=10 000 is the length of the McMC chain. Estimator μj is asymptotically normally distributed with mean p=0·1 and standard deviation ![]() , where V asymp=
, where V asymp=![]() , the limiting variance of
, the limiting variance of ![]() (Geyer, Reference Geyer1992). With independent draws, the sd of μj is
(Geyer, Reference Geyer1992). With independent draws, the sd of μj is ![]() . In our case, using the estimator of the asymptotic variance proposed by (Geyer, Reference Geyer1992), the sd of μj is approximately 0·0097 (similar figure for all j). The histogram reproduces very well this null distribution, suggesting that markers have no detectable effects at the level of the variance of back fat.
. In our case, using the estimator of the asymptotic variance proposed by (Geyer, Reference Geyer1992), the sd of μj is approximately 0·0097 (similar figure for all j). The histogram reproduces very well this null distribution, suggesting that markers have no detectable effects at the level of the variance of back fat.
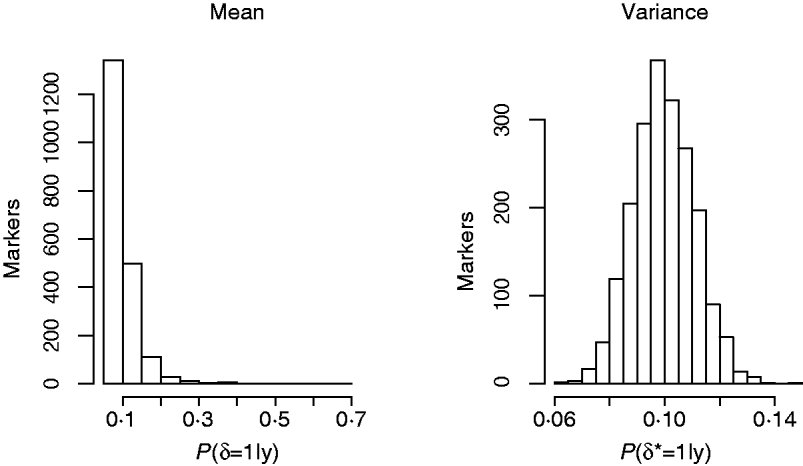
Fig. 4. Histograms of posterior probabilities of marker indicators from the GHETMIX model, across number of markers, at the level of the mean (left) and variance (right) for back fat data.
The posterior means of marker effects obtained from model GHET were investigated and found to be in good agreement with those from model GHETMIX. For example, the two largest posterior means from model GHETMIX are also the two largest from model GHET. The third, fourth and fifth largest from model GHETMIX correspond to the 13th, 12th and 9th largest from model GHET.
(iii) Model comparison
The third column of Table 2 shows Monte Carlo estimates of ∑ilog (CPOi) for the four models. The similarity of the estimates of ∑ilog (CPOi) for models GHOM and GHOMMIX (1205·0 and 1204·9) does not make it possible to discriminate between them. Increasing the complexity of the models by introducing variance heterogeneity due to the effects of markers does not improve the global fit. This result together with the evidence in Fig. 4 does not lend support to the presence of a detectable genetic component at the level of the residual variance.
Table 2. Monte Carlo estimates of ∑ilog (CPO i), of the correlation between observed and predicted data ![]() obtained from the cross-validation study, and of the measure of predictive ability at the level of the variance given by the average of expression (11), D, for the four genomic models fitted to back fat data, and different values of p. (τ2, c2τ2, τ*2, c*2τ*2) is (0·5×10−7, 0·1×10−3, 0·5×10−9, 0·2×10−5) for p=p*=0·1, (τ2, c2τ2) is (0·1×10−7,0·55×10−4) for p=0·2 and (0·5×10−7, 0·22×10−4) for p=0·5
obtained from the cross-validation study, and of the measure of predictive ability at the level of the variance given by the average of expression (11), D, for the four genomic models fitted to back fat data, and different values of p. (τ2, c2τ2, τ*2, c*2τ*2) is (0·5×10−7, 0·1×10−3, 0·5×10−9, 0·2×10−5) for p=p*=0·1, (τ2, c2τ2) is (0·1×10−7,0·55×10−4) for p=0·2 and (0·5×10−7, 0·22×10−4) for p=0·5

The bottom two rows in Table 2 show that global fit is hardly affected by changes in the tuning parameter p. Indeed, setting p equal to 0·2 or to 0·5 has little influence on the estimated values of ∑ilog (CPOi).
In addition to the four genomic models, three other models were fitted to the data: a simple model with only two parameters (mean μ and homogeneous variance σ2) of the form y|μ,σ2~N (μ, σ2), a pedigree based only infinitesimal homogeneous variance model with normally distributed genetic effects a of the form y i|μ, u i, σ2~N (μ+u i, σ2), u|σu2~N (0, Aσu2), and finally a genetically structured heterogeneous variance model with additive genetic effects affecting mean (u) and variance (u*), of the form y i|μ, u i, u i*, ~N (μ+u i, exp (μ*+u i*)), u, u*|G~N (0, A ⊗ G) as in Sorensen & Waagepetersen (Reference Sorensen and Waagepetersen2003), also pedigree based only. In this model, A is the additive genetic relationship matrix and G is the covariance matrix associated with the joint distribution [u, u*|G]. The ∑i log (CPOi) for these models were 1156·4, for the simple model, 1171·9 for the second and 1173·2 for the third. The models postulating a genetic component are better supported by the data, but once again there is no additional support for a genetic component at the level of the variance. All these models produce lower measures of global fit than the genomic models.
Estimates of posterior means (95% posterior intervals in brackets) of parameters based on pedigree information only from the genetically structured heterogeneous variance model were as follows. For the additive genetic variance at the level of the mean, 0·0073 (0·0032; 0·012), at the level of the variance, 0·10×10−3 (0·14×10−4; 0·28×10−3) (the estimate of the posterior mode is 0·47×10−4) and for the genetic correlation, 0·01 (−0·91; 0·98). The modal values of the prior distributions were, for the additive genetic variance at the level of the mean, 0·0034, at the level of the variance, 0·43×10−4, and the correlation was assumed to be uniformly distributed between −1 and 1. The posterior mode of the additive genetic variance at the level of the variance does not differ from the mode of the prior distribution, and the posterior distribution of the correlation coefficient is centred in the vicinity of zero, with a posterior uncertainty covering almost the whole support of the prior distribution, indicating no Bayesian learning from the data. These results are not in conflict with the absence of genetic variability at the level of the variance.
(iv) Genomic prediction
A six-fold cross-validation study was carried out allocating individuals randomly into six folds of equal size. The predicted phenotypes ![]() (f=1, …, 6) were obtained using estimates of parameters obtained by fitting the four models to data in which records from the fth fold were excluded. The predictive ability of a model was assessed by the average correlation (over the six folds) between observed and predicted phenotypes. The predictive ability of a model at the level of the residual variance was obtained by the average over the six folds of the quantity
(f=1, …, 6) were obtained using estimates of parameters obtained by fitting the four models to data in which records from the fth fold were excluded. The predictive ability of a model was assessed by the average correlation (over the six folds) between observed and predicted phenotypes. The predictive ability of a model at the level of the residual variance was obtained by the average over the six folds of the quantity
where ![]() and
and ![]() . In these expressions,
. In these expressions, ![]() ,
, ![]() ,
, ![]() ,
, ![]() are the posterior means of the model parameters.
are the posterior means of the model parameters.
The results in the last two columns of Table 2 reveal the same pattern as before, for the measure of global fit (third column of the table). Increasing the complexity of the models by inclusion of markers at the level of the variance does not improve the correlation between observed and predicted phenotypes and does not improve prediction at the level of the variance. These results are not affected by changes in the tuning parameter p.
The overall conclusion from the analysis is that a model postulating genetic heterogeneity of residual variance of back fat is not supported by the data. However, the analysis signals the existence of approximately five genomic regions with detectable effects on the trait at the level of the mean. As mentioned above, a limitation of the present analysis is that a polygenic effect was not included. This could have resulted in an overestimation of marker effects.
5. Discussion
Genomic models designed to detect QTL effects on the mean and variance were developed and McMC algorithms were constructed for their implementation. A study using simulated data with known QTL positions confirmed the ability of the genomic models to detect signals at the level of mean and variance. The strength of the signals clearly depends on the size of the effects and on whether the QTLs operate on mean or variance, with the expectation that detection of effects at the level of the variance may require a larger experiment than detection at the level of the mean. An approximation to the relative sizes of experiment needed can be arrived at as follows. Consider datum on individual i, y ki, carrying marker genotype 1 or 2, with effects a k on the mean (i=1, 2, …, n; k=1, 2), n replications per genotype. Individuals with genotype 1 have known residual variance σ2 and those with genotype 2 have residual variance σ2σa*2=σ*2, where σa*2 is unknown. Thus, individuals carrying genotype 2 have residual variance that is scaled by the factor σa*2 relative to the variance of individuals carrying genotype 1. Assuming normality of y ki|a k, the variance of the maximum likelihood estimator of a 1 is σ2/n and of a 2 is σ*2/n. The variance of the estimator of the difference Δm=a 2−a 1 is σ2 (1+σa*2)/n, and that of the estimator of σa*2 is 2 (σa*2) 2/n (the asymptotic variance of the variance is used for simplicity). Under the null hypothesis, Δm=0 at the level of the mean, and σa*2=1 at the level of the variance. Using standard calculations (for example, Chow et al., Reference Chow, Shao and Wang2008), the ratio of sample sizes required to detect QTL effects on mean and variance, assuming the same probabilities of type I error and the same power, is given by
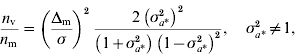
where n m (n v) is the sample size required to detect an effect on the mean (variance). The first term on the right-hand side specifies the standardized size of the difference to be detected at the level of the mean, and σa*2 specifies the size of the effect operating at the level of the variance. For Δm/σ=0·20 and 0·83<σa*2<1·23, σa*2≠1, the ratio is bigger than 1, indicating that for a large range of scenarios it is harder to detect effects on the variance. For example, setting Δm/σ=0·20 and σa*2=1·1, detecting effects on variance requires an experiment five times larger than on the mean. However, if Δm/σ=0·15 and σa*2=1·2, an approximate representation for simulated scenario 2, the ratio is 0·7, indicating that detection of effects on mean and variance is approximately equally demanding. Alternatively, given the same probabilities of type I error and the same power for detection at the level of mean and variance, for a given sample size, setting n m=n v, sizes of effects to be detected at the level of variance equal to σa*2=1·1, 1·3, 1·5, 2·0, would allow one to detect effects at the level of the mean equal to Δm/σ=0·09, 0·25, 0·37, 0·61, respectively. A detailed analysis on the statistical power to detect loci affecting environmental variance was recently reported by Visscher & Postuma Reference Visscher and Posthuma2010).
The analysis of back fat data does not provide support for a genetic component at the level of the environmental variance. In general, inferences at the level of the variance can be sensitive to the presence of skewness of the conditional distribution of the data. Ros et al., (Reference Ros, Sorensen, Waagepetersen, Dupont-Nivet, SanCristobal, Bonnet and Mallard2004) and Mulder et al., (Reference Mulder, Bijma and Hill2007) show that in a model with genetic components at the level of mean and variance, the skewness of the marginal distribution of the data is directly proportional to the correlation between additive genetic values affecting mean and variance. Therefore, if the distribution of the data is skewed in either direction not necessarily due to the presence of a genetically structured variance heterogeneity, such a model would fit relatively better than a standard model with homogeneous variance, and this would result in spurious inferences. Despite the negative results concerning the detection of marker effects on the variance, the distribution of residuals was investigated computing Monte Carlo estimates of the posterior distribution of the residual skewness. Results revealed no signs of asymmetry (data not shown).
The genomic models were implemented treating the variances of the mixture distributions and the probability parameter p as known parameters, to be tuned by the user. This was not a severe limitation. Once a rough estimate of the overall additive genetic variance at the level of the mean and variance (fitting pedigree based only infinitesimal models) is available, then the remaining parameters can easily be tuned. Measures of global fit are not sensitive to perturbations in p, as shown in Table 2. However an extension of the McMC algorithm that allows joint inferences of parameters avoiding tuning is in principle straightforward. For example, for the GHETMIX model, let σa2=c 2τ2, σa*2=c*2τ*2. Then the prior distributions of marker effects at the level of mean a j and variance a j* can be written as P(a j|δj, σa2)=δjN (0,σa2)+ (1−δj)N (0, σa2/k) and P(a j*|δj*,σa*2)=δj*N (0, σa*2)+ (1−δj*)N (0, σa*2/k), where the constant k is chosen to be equal to 1000, say, so that the components of the mixture have good discriminating ability. Assuming that the priors for σa2 and σa*2 are scaled inverse chi-square distributions, and a common beta distribution is assigned as prior for p and p*, then these two sets of prior distributions are conjugate for the respective fully conditional posterior distributions of σa2, σa*2, p and p* and updates are immediate via Gibbs steps. The remaining parameters are updated using the same strategy used with the GHETMIX model. The algorithm is therefore easy to construct but, in general, the behaviour of the resulting Markov chain will be influenced by the structure of the data and the properties of the trait analysed.








